---

🎓 Tutorial: Introduction to Machine Learning – Learning Paradigms – PAC Learning

---

🧠 1. What is Machine Learning?

Machine Learning (ML) is a subfield of artificial intelligence (AI) that focuses on building systems that learn from data to make decisions or predictions without being explicitly programmed.

Arthur Samuel’s definition (1959):

“Machine Learning is the field of study that gives computers the ability to learn without being explicitly programmed.”

---

🎯 2. Goals of Machine Learning

• Discover patterns in data
• Make predictions on unseen data
• Improve performance with experience
• Generalize well to new situations

---

📚 3. Learning Paradigms in ML

Machine learning problems can be broadly classified into three learning paradigms based on the supervision in training data:

✅ 3.1 Supervised Learning

• Input: Labeled dataset (X, Y)
• Goal: Learn a function f : X → Y to map input to output
• Examples:
  • Classification (e.g., spam detection)
  • Regression (e.g., house price prediction)

❓ 3.2 Unsupervised Learning

• Input: Unlabeled dataset (X)
• Goal: Discover structure or patterns in data
• Examples:
  • Clustering (e.g., customer segmentation)
  • Dimensionality reduction (e.g., PCA)

⚖️ 3.3 Reinforcement Learning

• Input: Environment and rewards
• Goal: Learn to make sequences of decisions to maximize reward
• Examples:
  • Game playing (e.g., AlphaGo)
  • Robotics (e.g., walking, grasping)

🧪 3.4 Semi-Supervised Learning

• Mix of labeled and unlabeled data
• Useful when labeling is expensive

🧑‍🤝‍🧑 3.5 Self-Supervised Learning

• Learns supervision signal from the data itself (e.g., predicting missing words in a sentence)

---

4. PAC LEARNING

Concept / Term	Definition / Explanation
Instance Space (𝑿)	The set of all possible input examples. In PAC learning, typically: 𝑋 = {0,1}ⁿ — all binary vectors of length n.
Concept / Target Function (𝒄)	The unknown function we aim to learn. It maps instances to labels: 𝑐 : X → {0,1}.
Hypothesis Class (𝑯)	A set of possible functions (hypotheses) that the learning algorithm can choose from: H ⊆ 2ˣ, meaning each hypothesis h ∈ H maps instances to {0,1}.
Distribution (𝑫)	An unknown probability distribution over the instance space 𝑋. The training data is drawn i.i.d. from this distribution.
Training Examples	A sequence of labeled examples drawn i.i.d. from 𝑫: (x₁, c(x₁)), …, (xₘ, c(xₘ)).
Learning Algorithm (𝑨)	The algorithm that receives training data and returns a hypothesis h ∈ H that approximates the target function c.
PAC Guarantee	The output hypothesis h satisfies: Prₓ∼𝑫[h(x) ≠ c(x)] ≤ ε with probability at least 1 − δ.
ε (epsilon)	The accuracy parameter — how close the hypothesis should be to the target function. Smaller ε means higher accuracy.
δ (delta)	The confidence parameter — how confident we want to be that the learning algorithm will return a good hypothesis.
PAC (Probably Approximately Correct)	“Probably” = with probability ≥ 1 − δ, “Approximately Correct” = error ≤ ε.
PAC Learnability	A concept class C is PAC-learnable if there exists a polynomial-time algorithm that for any ε, δ ∈ (0,1), can return a hypothesis with PAC guarantees.
Sample Complexity (𝒎)	The number of training examples needed to achieve PAC guarantees. Formula (with VC dimension): m = O(VCdim(H) ⋅ log(1/ε) + log(1/δ))
VC Dimension (VCdim(H))	The Vapnik-Chervonenkis dimension — a measure of the capacity/complexity of the hypothesis class H.
One-sided Error	Hypothesis never makes false positives (i.e., always predicts 0 for negative instances).
Two-sided Error	Errors are allowed on both positive and negative examples.

Probably Approximately Correct (PAC) learning is a foundational framework in computational learning theory, introduced by Leslie Valiant, that formalizes the concept of learnability from a theoretical, algorithmic perspective. It defines learning as the process of inferring a hypothesis that closely approximates an unknown target concept based on randomly drawn labeled examples, without relying on explicit programming. A concept class is considered PAC-learnable if a learning algorithm can, with high probability, produce a hypothesis that performs well on unseen data, using only a feasible (polynomial) number of training examples and computational steps. The framework assumes the presence of an unknown data distribution and allows the learner to receive examples either passively (as positive instances) or actively through queries to an oracle. Crucially, PAC learning emphasizes generalization: the learned hypothesis must not just fit the training data but should also perform well on new instances from the same distribution. The theory identifies specific classes of Boolean functions—such as bounded CNF and monotone DNF expressions—that are efficiently learnable, while also highlighting inherent limitations due to computational intractability and cryptographic hardness in learning more complex or unrestricted functions. Extensions to the PAC model address practical concerns like noise in data, real-valued outputs, and domain-specific biases, while the notion of VC dimension helps quantify the capacity of a hypothesis space and determine the number of examples needed for learning. Overall, PAC learning offers a rigorous, probability-based approach to understanding what can be learned, how efficiently it can be learned, and under what conditions learning is possible.

---

VC Dimension

🔍 Definition

The Vapnik–Chervonenkis (VC) Dimension is a fundamental measure of the capacity or expressiveness of a hypothesis class (denoted as 𝓗). It quantifies how well a model can fit various labelings of data.

---

💡 Key Concepts

Concept	Description
Shattering	A set of points is shattered by hypothesis class 𝓗 if 𝓗 can realize all possible labelings (2ⁿ combinations for n points).
VC Dimension	The maximum number of points that can be shattered by 𝓗. Denoted as VC(𝓗).
Intuition	Measures the ability of 𝓗 to fit any training data perfectly. Higher VC means higher complexity.
Zero Error Bound	If a hypothesis from 𝓗 achieves zero error on N examples, then N ≤ VC(𝓗).

---

📊 Example Interpretation

• If VC(𝓗) = 3, then:
  • 𝓗 can shatter any configuration of 3 points.
  • It cannot shatter all configurations of 4 points.

---

🧠 Why It Matters

• A core concept in statistical learning theory.
• Helps balance model complexity vs. overfitting.
• Used to understand generalization in machine learning.

---

📘 Historical Note

• Introduced by Vladimir Vapnik and Alexey Chervonenkis.
• Applicable to binary classifiers, geometric set families, and more.

---

Vapnik, V. N., & Chervonenkis, A. Y. (2015). On the uniform convergence of relative frequencies of events to their probabilities. In Measures of complexity: festschrift for alexey chervonenkis (pp. 11-30). Cham: Springer International Publishing.

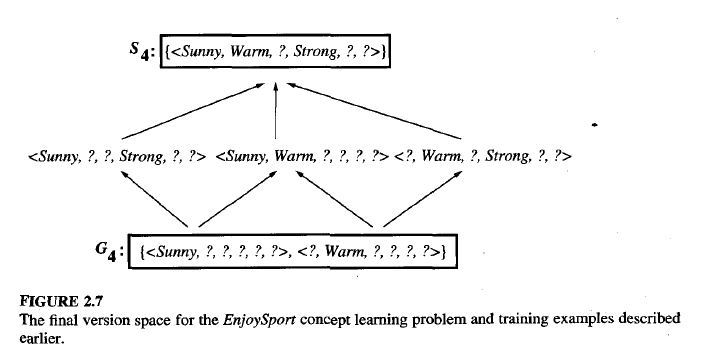
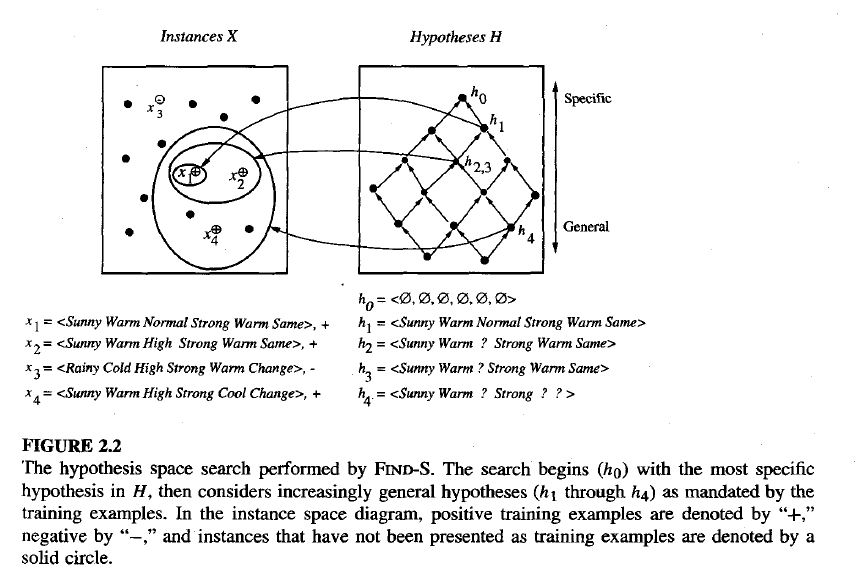
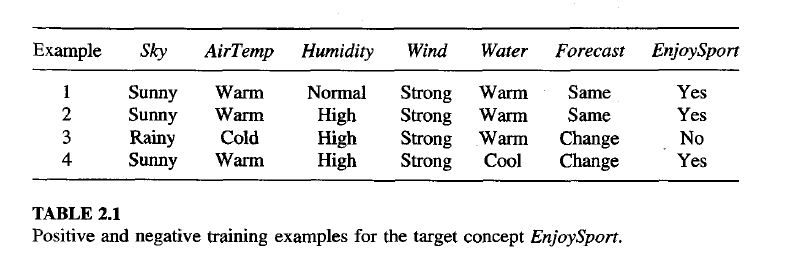
FIND-S: FINDING A MAXIMALLY SPECIFIC HYPOTHESIS

(Ref : Mitchell, T. M. (1997). Machine Learning. McGraw-Hill.)

A Systematic Approach to Learning with the Candidate Elimination Algorithm

---

Revisit again : Candidate Elimination Algorithm — Simple Steps

Step 1 – Initialization

• S = most specific hypothesis (matches nothing yet)
• G = most general hypothesis (matches everything)

---

Step 2 – Process each training example:

When the example is Positive (Yes)

1. Adjust S so it becomes just general enough to include this example.
2. Remove from G any hypothesis that does not include this example.

---

When the example is Negative (No)

1. Remove from S any hypothesis that still includes this example.
2. Specialize each hypothesis in G that includes this example, just enough to exclude it, while still including all positive examples so far.
3. Remove any hypotheses from G that are more specific than others or duplicate.

---

Step 3 – Completion

• After all examples are processed, the version space is the set of hypotheses between S and G.
• S represents the narrowest possible rule consistent with the data.
• G represents the broadest possible rule consistent with the data.

---