- Randomized Algorithms
- QuickSort’s Time Complexities : Average case, Best Case, Worst Case
- Partitioning technique : Balanced and Imbalanced
- Randomized QuickSort
- Worst and average case time complexities of Randomized QuickSort
- Finding expected running time of Randomized Quick Sort.
- Randomized Primality Testing
- Fermat’s primality testing
- Miller–Rabin primality testing(Randomized version)
- Freivalds’ Algorithm for Matrix Multiplication : randomized algorithm for verification of matrix multiplication
- Randomized algorithm solution for Hiring Problem
Randomized Algorithm
Expected Running time of Randomized QuickSort
What is Randomized Algorithms?
- A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure.
- The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the “average case” over all possible choices of random determined by the random bits; thus either the running time, or the output (or both) are random variables.

Applications of Randomized Algorithms
- Determining outcomes in games
- Preventing communications on a shared channel from interfering with each other
- Initializing passwords
- Performing statistical (e.g. “Monte Carlo”) analysis on a system
- Simulating real-world behaviors and processes
- Emergent system generation using genetic hybridization
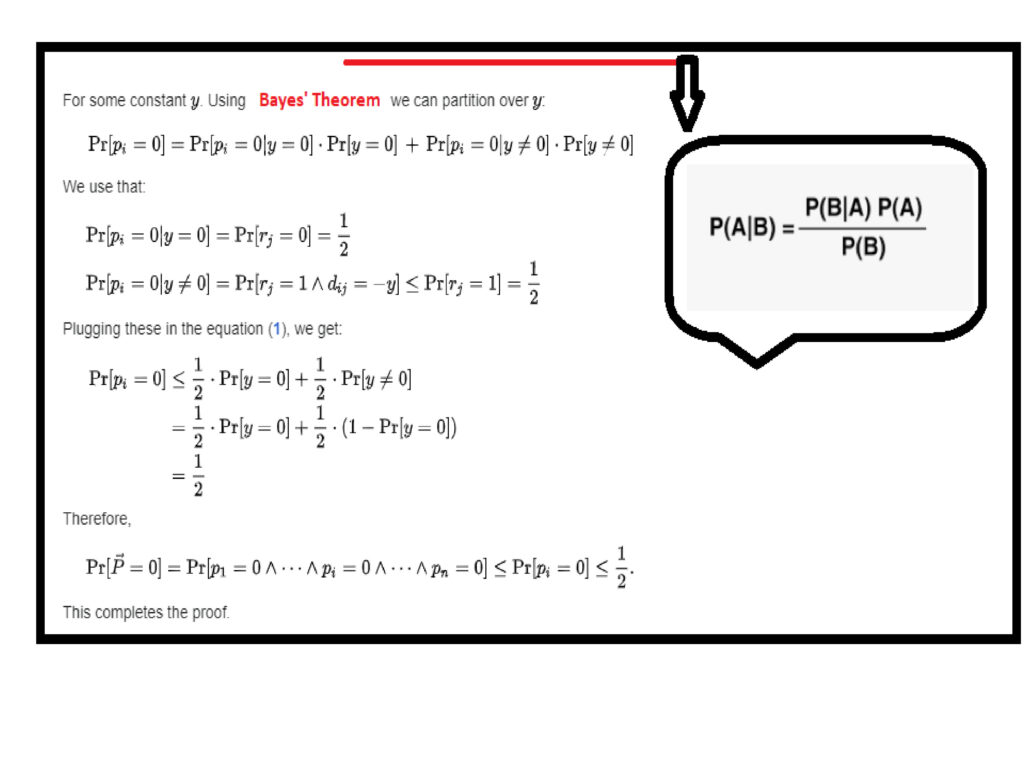
Types of Randomized Algorithms
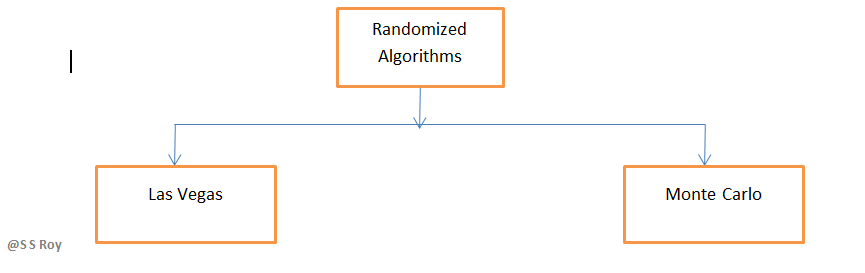
A Las Vegas algorithm always produces the correct result, but its running time is based on a random value. A Monte Carlo algorithm has a deterministic running time and produces an answer that has a probability of ≥ 1/3 of being correct.
The Las Vegas method of randomized algorithms never gives incorrect outputs, making the time constraint as the random variable. For example, in string matching algorithms, Las Vegas algorithms start from the beginning once they encounter an error. This increases the probability of correctness. Eg., Randomized Quick Sort Algorithm.
The Monte Carlo method of randomized algorithms focuses on finishing the execution within the given time constraint. Therefore, the running time of this method is deterministic. For example, in string matching, if monte carlo encounters an error, it restarts the algorithm from the same point. Thus, saving time. Eg., Karger’s Minimum Cut Algorithm.
Randomized Quick Sort









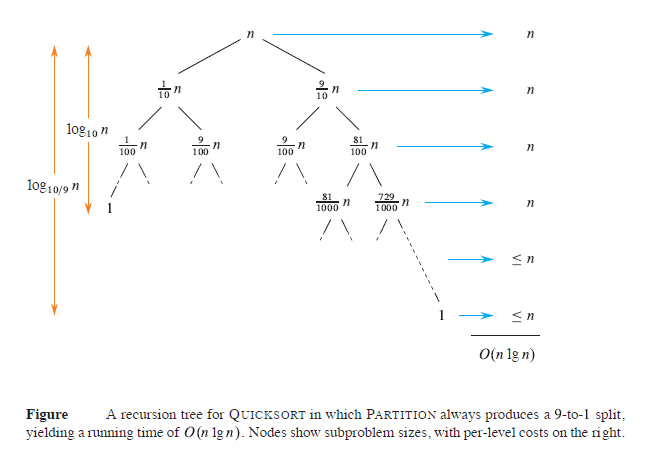

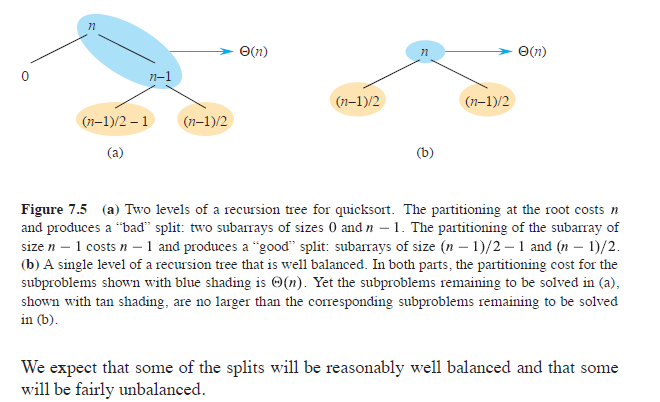







Primality testing








Freivalds’ Algorithm for Matrix Multiplication : randomized algorithm for verification of matrix multiplication