- Flow Network & its components
- Maximum Flow
- Dijkstra’s algorithm
- Dijkstra’s Vs Bellman-Ford algorithm
- Bellman-Ford algorithm
- How Bellman-Ford works?
- Ford Fulkerson Algorithm
- Edmond Karp Algorithm
- Push Relabel Algorithm
- Floyd Warshall Algorithm
- MaxFlow Min Cut
- Bipartite Matching
- Cycle Cancellation Algorithm
A flow network, also known as a network flow, is a directed graph where each edge has a capacity and each node (except for the source and sink nodes) has a flow value associated with it. Flow networks are commonly used to model transportation or distribution systems, such as water distribution networks, traffic flow, or computer networks.
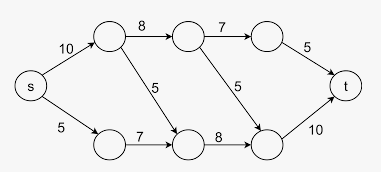
Fig.An example of flow network with Source and Sink node with capacities of each link
In a flow network:
- Nodes: These represent points in the network where the flow can split or merge. Typically, there are two special nodes: a source node, from which flow originates, and a sink node, where flow terminates.
- Edges: These represent the connections between nodes and have associated capacities, which indicate the maximum amount of flow that can traverse the edge.
- Flow: This is the amount of material, information, or whatever is being transported, that is sent from the source to the sink through the network. The flow must satisfy certain constraints:
- The flow through any edge cannot exceed its capacity.
- The total flow out of any node (except the source and sink) must equal the total flow into that node.
Flow networks are used in optimization problems, such as the maximum flow problem, where the goal is to determine the maximum amount of flow that can be sent from the source to the sink without violating the capacity constraints. They also find applications in various fields including transportation planning, telecommunications, and logistics.
Dijkstra’s Vs Bellman-Ford algorithm
Bellman-Ford algorithm

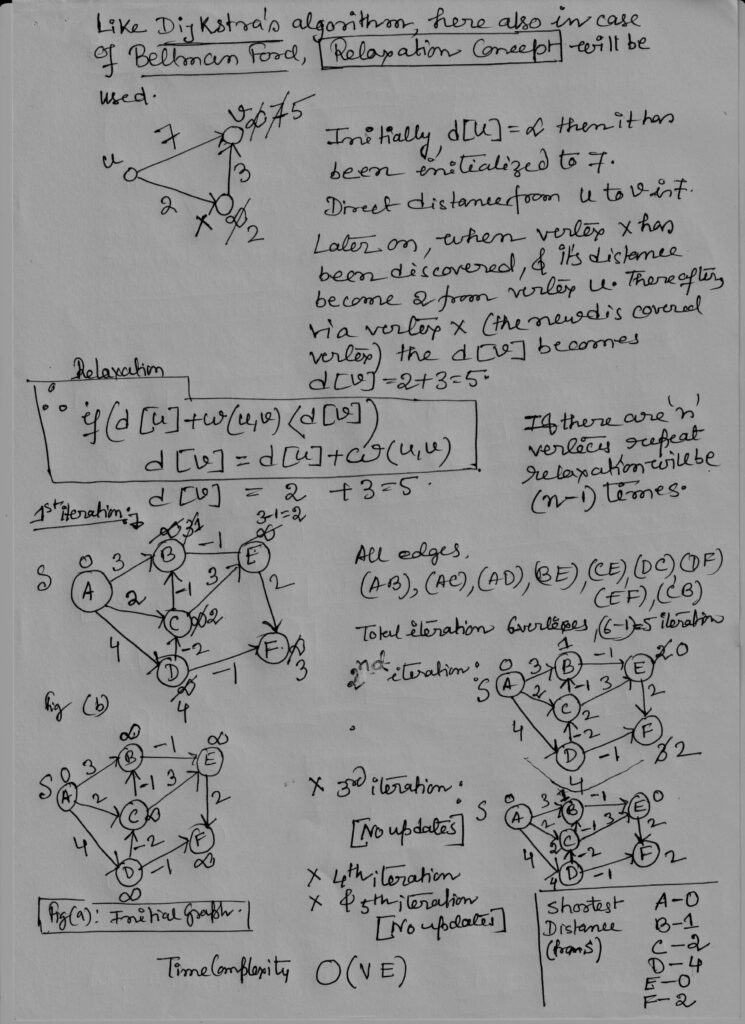
How Does Bellman-Ford Work?
Ford Fulkerson Algorithm

Edmond Karp Algorithm
The algorithm is identical to the Ford–Fulkerson algorithm, except that the search order when finding the augmenting path is defined. The path found must be a shortest path that has available capacity. This can be found by a breadth-first search, where we apply a weight of 1 to each edge. The running time of 



Push Relabel Algorithm
In mathematical optimization, the push–relabel algorithm (alternatively, preflow–push algorithm) is an algorithm for computing maximum flows in a flow network. The name “push–relabel” comes from the two basic operations used in the algorithm. Throughout its execution, the algorithm maintains a “preflow” and gradually converts it into a maximum flow by moving flow locally between neighboring nodes using push operations under the guidance of an admissible network maintained by relabel operations. In comparison, the Ford–Fulkerson algorithm performs global augmentations that send flow following paths from the source all the way to the sink.
Ford Fulkerson
The Ford-Fulkerson algorithm is used to compute the maximum flow in a flow network. It works by repeatedly finding augmenting paths in the residual graph and increasing the flow along those paths. This method can be implemented with DFS (Depth-First Search) or BFS (Breadth-First Search) for finding augmenting paths. Here, we’ll use DFS for simplicity in the explanation.
//C code for Ford-Fulkerson algorithm
#include <stdio.h>
#include <limits.h> // For INT_MAX (used to represent infinity)
#include <string.h> // For memset function
// Maximum number of vertices in the graph
#define V 6 // You can change this to modify the number of vertices
// Function to perform Depth-First Search (DFS) in the residual graph
// It will find an augmenting path from source to sink and update the parent array
int dfs(int residualGraph[V][V], int source, int sink, int parent[], int visited[]) {
// Mark the source node as visited
visited[source] = 1;
// If we reach the sink, return true (path found)
if (source == sink) {
return 1;
}
// Try all adjacent vertices of the current vertex
for (int v = 0; v < V; v++) {
// If v is not visited and there is a positive capacity (residual capacity)
if (!visited[v] && residualGraph[source][v] > 0) {
parent[v] = source; // Set the parent of v as the current vertex
// Recur to explore further
if (dfs(residualGraph, v, sink, parent, visited)) {
return 1; // If augmenting path is found, return true
}
}
}
// If no augmenting path is found, return false
return 0;
}
// Function to implement the Ford-Fulkerson algorithm
int fordFulkerson(int graph[V][V], int source, int sink) {
// Create a residual graph and initialize it as the input graph
int residualGraph[V][V];
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
residualGraph[i][j] = graph[i][j];
}
}
int parent[V]; // Array to store the path
int maxFlow = 0; // Variable to store the maximum flow
// Augment the flow while there is an augmenting path
while (1) {
// Visited array to keep track of visited nodes during DFS
int visited[V] = {0};
// Perform DFS to find an augmenting path
if (!dfs(residualGraph, source, sink, parent, visited)) {
break; // No more augmenting path, break the loop
}
// Find the maximum flow in the found path
int pathFlow = INT_MAX;
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
pathFlow = (pathFlow < residualGraph[u][v]) ? pathFlow : residualGraph[u][v];
}
// Update the residual graph by subtracting the flow from forward edges
// and adding the flow to the reverse edges
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
residualGraph[u][v] -= pathFlow;
residualGraph[v][u] += pathFlow;
}
// Add the flow of the current path to the overall flow
maxFlow += pathFlow;
}
return maxFlow; // Return the maximum flow found
}
int main() {
// Example graph (6 vertices)
// Graph represented as an adjacency matrix (capacity matrix)
int graph[V][V] = {
{0, 16, 13, 0, 0, 0}, // Vertex 0 connects to 1 with capacity 16, 2 with capacity 13
{0, 0, 10, 12, 0, 0}, // Vertex 1 connects to 2 with capacity 10, 3 with capacity 12
{0, 4, 0, 0, 14, 0}, // Vertex 2 connects to 1 with capacity 4, 4 with capacity 14
{0, 0, 9, 0, 0, 20}, // Vertex 3 connects to 2 with capacity 9, 5 with capacity 20
{0, 0, 0, 7, 0, 4}, // Vertex 4 connects to 3 with capacity 7, 5 with capacity 4
{0, 0, 0, 0, 0, 0} // Vertex 5 is the sink (no outgoing edges)
};
int source = 0; // Source node (vertex 0)
int sink = 5; // Sink node (vertex 5)
// Calling the Ford-Fulkerson algorithm to find the maximum flow
int maxFlow = fordFulkerson(graph, source, sink);
// Output the maximum flow
printf("The maximum flow from source %d to sink %d is %d\n", source, sink, maxFlow);
return 0;
}
Output :
The maximum flow from source 0 to sink 5 is 23Here’s below the complete C++ code for implementing the Ford-Fulkerson algorithm using classes and the Standard Template Library (STL). Each line is explained with comments.
// C++ code for implementing the Ford-Fulkerson
#include <iostream>
#include <vector>
#include <queue>
#include <climits> // For INT_MAX
using namespace std;
// Class to represent a graph
class Graph {
private:
int numVertices; // Number of vertices in the graph
vector<vector<int>> capacity; // Capacity matrix
public:
// Constructor to initialize the graph
Graph(int vertices) : numVertices(vertices) {
capacity.resize(vertices, vector<int>(vertices, 0));
}
// Function to add an edge with a given capacity
void addEdge(int u, int v, int cap) {
capacity[u][v] = cap; // Set the capacity of the edge from u to v
}
// Function to perform BFS and find an augmenting path
bool bfs(vector<vector<int>> &residualCapacity, int source, int sink, vector<int> &parent) {
vector<bool> visited(numVertices, false); // Keep track of visited vertices
queue<int> q; // Queue for BFS
q.push(source);
visited[source] = true;
parent[source] = -1; // Source has no parent
while (!q.empty()) {
int u = q.front();
q.pop();
// Explore all neighbors of u
for (int v = 0; v < numVertices; v++) {
// If v is not visited and there is residual capacity
if (!visited[v] && residualCapacity[u][v] > 0) {
q.push(v);
visited[v] = true;
parent[v] = u; // Set parent of v to u
// If we reach the sink, return true
if (v == sink)
return true;
}
}
}
// If no path to sink is found
return false;
}
// Function to implement the Ford-Fulkerson algorithm
int fordFulkerson(int source, int sink) {
vector<vector<int>> residualCapacity = capacity; // Create a residual capacity matrix
vector<int> parent(numVertices); // To store the augmenting path
int maxFlow = 0; // Initialize the max flow to 0
// While there exists an augmenting path
while (bfs(residualCapacity, source, sink, parent)) {
// Find the minimum residual capacity in the augmenting path
int pathFlow = INT_MAX;
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
pathFlow = min(pathFlow, residualCapacity[u][v]);
}
// Update the residual capacities of the edges and reverse edges
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
residualCapacity[u][v] -= pathFlow;
residualCapacity[v][u] += pathFlow;
}
// Add the path flow to the overall flow
maxFlow += pathFlow;
}
return maxFlow;
}
};
int main() {
// Create a graph with 6 vertices (0 to 5)
Graph g(6);
// Add edges along with their capacities
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 12);
g.addEdge(2, 1, 4);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
// Display the maximum flow from source (0) to sink (5)
cout << "The maximum possible flow is: " << g.fordFulkerson(0, 5) << endl;
return 0;
}
Output :
The maximum possible flow is: 23Here below is a C code implementation of the Edmond Karp, with detailed explanations for each line within the code:
//C Code for Edmonds-Karp Algorithm:
#include <stdio.h>
#include <limits.h> // To use INT_MAX for infinite capacity
#include <queue> // For BFS (using STL queue for simple implementation)
// Number of vertices in the graph
#define V 6 // Example graph with 6 vertices (adjust as necessary)
// Function to perform BFS and find the path with available capacity
int bfs(int residualGraph[V][V], int source, int sink, int parent[]) {
// Initialize all nodes as not visited
bool visited[V] = {0};
// Create a queue for BFS
std::queue<int> q;
// Start BFS from the source
q.push(source);
visited[source] = true;
parent[source] = -1; // Source has no parent
// BFS to find an augmenting path from source to sink
while (!q.empty()) {
int u = q.front();
q.pop();
// Traverse all adjacent vertices of u
for (int v = 0; v < V; v++) {
if (visited[v] == false && residualGraph[u][v] > 0) { // If v is not visited and has capacity left
q.push(v);
parent[v] = u; // Set parent of v as u
visited[v] = true;
// If we reached the sink, no need to go further
if (v == sink) {
return 1; // Return true if we found a path
}
}
}
}
return 0; // Return false if no augmenting path exists
}
// Function to implement the Edmonds-Karp algorithm
int edmondsKarp(int graph[V][V], int source, int sink) {
// Create a residual graph and initialize it as the input graph
int residualGraph[V][V];
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
residualGraph[i][j] = graph[i][j];
}
}
int parent[V]; // Array to store the path
int maxFlow = 0; // Variable to store the maximum flow
// Augment the flow while there is a path from source to sink
while (bfs(residualGraph, source, sink, parent)) {
// Find the maximum flow in the found path
int pathFlow = INT_MAX;
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
pathFlow = (pathFlow < residualGraph[u][v]) ? pathFlow : residualGraph[u][v];
}
// Update the residual graph by subtracting the flow from forward edges
// and adding the flow to the reverse edges
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
residualGraph[u][v] -= pathFlow;
residualGraph[v][u] += pathFlow;
}
// Add the path flow to the overall flow
maxFlow += pathFlow;
}
return maxFlow; // Return the maximum flow found
}
// Main function to test the Edmonds-Karp algorithm
int main() {
// Example graph with 6 vertices (0 to 5)
// Graph represented as an adjacency matrix
int graph[V][V] = {
{0, 16, 13, 0, 0, 0}, // Vertex 0 is connected to 1 (capacity 16), 2 (capacity 13)
{0, 0, 10, 12, 0, 0}, // Vertex 1 is connected to 2 (capacity 10), 3 (capacity 12)
{0, 4, 0, 0, 14, 0}, // Vertex 2 is connected to 1 (capacity 4), 4 (capacity 14)
{0, 0, 9, 0, 0, 20}, // Vertex 3 is connected to 2 (capacity 9), 5 (capacity 20)
{0, 0, 0, 7, 0, 4}, // Vertex 4 is connected to 3 (capacity 7), 5 (capacity 4)
{0, 0, 0, 0, 0, 0} // Vertex 5 is connected to no one (sink)
};
int source = 0; // Source node (vertex 0)
int sink = 5; // Sink node (vertex 5)
// Calling the Edmonds-Karp algorithm to find the maximum flow
int maxFlow = edmondsKarp(graph, source, sink);
// Output the maximum flow
printf("The maximum flow from source %d to sink %d is %d\n", source, sink, maxFlow);
return 0;
}
Output :
The maximum flow from source 0 to sink 5 is 23//C++ Code with Class and Vector STL:
#include <iostream>
#include <vector>
#include <queue>
#include <limits.h> // For INT_MAX
using namespace std;
class EdmondsKarp {
private:
int V; // Number of vertices
vector<vector<int>> graph; // Adjacency matrix (graph representation)
// Helper function to perform BFS and find the augmenting path
bool bfs(vector<vector<int>>& residualGraph, int source, int sink, vector<int>& parent) {
vector<bool> visited(V, false);
queue<int> q;
q.push(source);
visited[source] = true;
parent[source] = -1;
// Perform BFS to find an augmenting path from source to sink
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v = 0; v < V; v++) {
// If the vertex is not visited and there is remaining capacity
if (!visited[v] && residualGraph[u][v] > 0) {
q.push(v);
parent[v] = u;
visited[v] = true;
// If we reached the sink, stop
if (v == sink) {
return true;
}
}
}
}
return false; // No augmenting path found
}
public:
// Constructor to initialize the graph with a given number of vertices
EdmondsKarp(int vertices) : V(vertices) {
graph.resize(V, vector<int>(V, 0)); // Initialize graph with 0s
}
// Function to set the capacities of edges (graph initialization)
void setEdge(int u, int v, int capacity) {
graph[u][v] = capacity;
}
// Function to implement the Edmonds-Karp algorithm
int edmondsKarp(int source, int sink) {
// Create a residual graph initially as a copy of the input graph
vector<vector<int>> residualGraph = graph;
vector<int> parent(V); // Array to store the path
int maxFlow = 0; // Variable to store the maximum flow
// Augment the flow while there is an augmenting path
while (bfs(residualGraph, source, sink, parent)) {
// Find the maximum flow in the found path
int pathFlow = INT_MAX;
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
pathFlow = min(pathFlow, residualGraph[u][v]); // Get the minimum capacity in the path
}
// Update the residual graph
for (int v = sink; v != source; v = parent[v]) {
int u = parent[v];
residualGraph[u][v] -= pathFlow; // Reduce the capacity of the forward edge
residualGraph[v][u] += pathFlow; // Increase the capacity of the reverse edge
}
// Add the flow of the current path to the total flow
maxFlow += pathFlow;
}
return maxFlow; // Return the total maximum flow
}
};
int main() {
int V = 6; // Number of vertices in the graph
EdmondsKarp ek(V); // Create an object of EdmondsKarp class
// Set edges and their capacities (graph initialization)
ek.setEdge(0, 1, 16);
ek.setEdge(0, 2, 13);
ek.setEdge(1, 2, 10);
ek.setEdge(1, 3, 12);
ek.setEdge(2, 1, 4);
ek.setEdge(2, 4, 14);
ek.setEdge(3, 2, 9);
ek.setEdge(3, 5, 20);
ek.setEdge(4, 3, 7);
ek.setEdge(4, 5, 4);
int source = 0; // Source node
int sink = 5; // Sink node
// Find the maximum flow
int maxFlow = ek.edmondsKarp(source, sink);
// Output the maximum flow
cout << "The maximum flow from source " << source << " to sink " << sink << " is " << maxFlow << endl;
return 0;
}
Output :
The maximum flow from source 0 to sink 5 is 23What is all pairs shortest path?
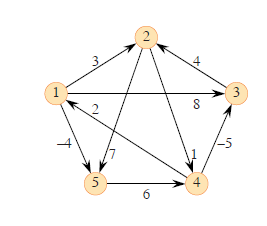
An example of the all-pairs shortest path problem can be illustrated with a simple weighted directed graph representing a road network. Consider the following graph:

In this graph:
- Vertices: There are four vertices labeled from 1 to 4.
- Edges: Each edge is weighted, representing the distance between connected vertices.
For example:
- There is an edge from vertex 1 to vertex 3 with weight 4.
- There is an edge from vertex 1 to vertex 2 with weight 1.
The task is to find the shortest path between every pair of vertices in this graph.
Floyd Warshall Algorithm
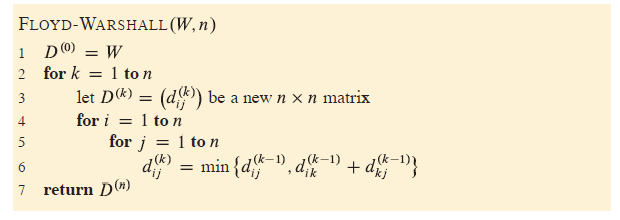


Floyd Warshall
//Here is the C program implementing the Floyd-Warshall algorithm
//with comments explaining each part of the code:
#include <stdio.h>
#include <limits.h>
#define MAX 10 // Defining the maximum size for the matrix (number of vertices)
// Function to implement the Floyd-Warshall algorithm
void floydWarshall(int dist[MAX][MAX], int n) {
// k is the intermediate node, i is the source node, and j is the destination node
for (int k = 0; k < n; k++) { // Loop over each intermediate node
for (int i = 0; i < n; i++) { // Loop over each source node
for (int j = 0; j < n; j++) { // Loop over each destination node
// If the path through the intermediate node k is shorter, update the distance
if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
// Function to print the distance matrix
void printSolution(int dist[MAX][MAX], int n) {
printf("The shortest distances between every pair of vertices are:\n");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][j] == INT_MAX) {
printf("INF "); // If no path exists, print INF
} else {
printf("%d ", dist[i][j]);
}
}
printf("\n");
}
}
int main() {
int n, i, j;
// Take input for number of vertices in the graph
printf("Enter the number of vertices: ");
scanf("%d", &n);
// Create the distance matrix (initialize with INT_MAX where there is no direct path)
int dist[MAX][MAX];
printf("Enter the adjacency matrix (use 0 for no direct edge and other positive values for edge weights):\n");
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
scanf("%d", &dist[i][j]);
// If there is no direct edge, set distance to INF (INT_MAX)
if (dist[i][j] == 0 && i != j) {
dist[i][j] = INT_MAX;
}
}
}
// Call the Floyd-Warshall algorithm
floydWarshall(dist, n);
// Print the result
printSolution(dist, n);
return 0;
}
Output :
Enter the number of vertices: 4
Enter the adjacency matrix (use 0 for no direct edge and other positive values for edge weights):
0 3 0 0
3 0 4 0
0 4 0 2
0 0 2 0
The shortest distances between every pair of vertices are:
0 3 7 5
3 0 4 6
7 4 0 2
5 6 2 0 /*To display not only the shortest distances and the vertices involved in the
shortest paths but also the total cost (the total distance) of each shortest path, we will update the program further.We need to modify the following: Track the shortest paths and their costs. Print the shortest path from one vertex to another, showing the intermediate vertices and the total cost.*/
#include <stdio.h>
#include <limits.h>
#define MAX 10 // Defining the maximum size for the matrix (number of vertices)
// Function to implement the Floyd-Warshall algorithm
void floydWarshall(int dist[MAX][MAX], int next[MAX][MAX], int n) {
// k is the intermediate node, i is the source node, and j is the destination node
for (int k = 0; k < n; k++) { // Loop over each intermediate node
for (int i = 0; i < n; i++) { // Loop over each source node
for (int j = 0; j < n; j++) { // Loop over each destination node
// If the path through the intermediate node k is shorter, update the distance
if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
next[i][j] = next[i][k]; // Update the next vertex on the shortest path
}
}
}
}
}
// Function to print the distance matrix
void printSolution(int dist[MAX][MAX], int next[MAX][MAX], int n) {
printf("The shortest distances between every pair of vertices are:\n");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][j] == INT_MAX) {
printf("INF "); // If no path exists, print INF
} else {
printf("%d ", dist[i][j]);
}
}
printf("\n");
}
// Now print the shortest paths and total cost
printf("\nShortest paths between every pair of vertices (with total cost) are:\n");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j) {
printf("Shortest path from %d to %d: ", i + 1, j + 1);
int current = i;
int totalCost = 0;
// Traverse the path and calculate total cost
while (current != j) {
printf("%d -> ", current + 1);
totalCost += dist[current][next[current][j]]; // Add the cost of the edge
current = next[current][j];
}
totalCost += dist[current][j]; // Add the cost from last node to the destination
printf("%d | Total cost: %d\n", j + 1, totalCost);
}
}
}
}
int main() {
int n, i, j;
// Take input for number of vertices in the graph
printf("Enter the number of vertices: ");
scanf("%d", &n);
// Create the distance matrix (initialize with INT_MAX where there is no direct path)
int dist[MAX][MAX];
int next[MAX][MAX];
printf("Enter the adjacency matrix (use 0 for no direct edge and other positive values for edge weights):\n");
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
scanf("%d", &dist[i][j]);
// Initialize next matrix to help in path reconstruction
if (dist[i][j] != 0 && dist[i][j] != INT_MAX) {
next[i][j] = j; // If there's an edge, set next[i][j] as j
} else if (i == j) {
next[i][j] = i; // For diagonal, the next node is itself
} else {
next[i][j] = -1; // No path initially
}
// If there is no direct edge, set distance to INF
if (dist[i][j] == 0 && i != j) {
dist[i][j] = INT_MAX;
next[i][j] = -1;
}
}
}
// Call the Floyd-Warshall algorithm
floydWarshall(dist, next, n);
// Print the result
printSolution(dist, next, n);
return 0;
}
Output :
Enter the number of vertices: 4
Enter the adjacency matrix (use 0 for no direct edge and other positive values for edge weights):
0 3 0 0
3 0 4 0
0 4 0 2
0 0 2 0
The shortest distances between every pair of vertices are:
0 3 7 5
3 0 4 6
7 4 0 2
5 6 2 0
Shortest paths between every pair of vertices (with total cost) are:
Shortest path from 1 to 2: 1 -> 2 | Total cost: 3
Shortest path from 1 to 3: 1 -> 2 -> 3 | Total cost: 7
Shortest path from 1 to 4: 1 -> 2 -> 3 -> 4 | Total cost: 5
Shortest path from 2 to 1: 2 -> 1 | Total cost: 3
Shortest path from 2 to 3: 2 -> 3 | Total cost: 4
Shortest path from 2 to 4: 2 -> 3 -> 4 | Total cost: 6
Shortest path from 3 to 1: 3 -> 2 -> 1 | Total cost: 7
Shortest path from 3 to 2: 3 -> 2 | Total cost: 4
Shortest path from 3 to 4: 3 -> 4 | Total cost: 2
Shortest path from 4 to 1: 4 -> 3 -> 2 -> 1 | Total cost: 5
Shortest path from 4 to 2: 4 -> 3 -> 2 | Total cost: 6
Shortest path from 4 to 3: 4 -> 3 | Total cost: 2
//C++ Code Using Class and Vector STL:
#include <iostream>
#include <vector>
#include <limits.h>
using namespace std;
class FloydWarshall {
private:
vector<vector<int>> dist; // Distance matrix (using vector of vectors)
int n; // Number of vertices
public:
// Constructor to initialize the number of vertices and the distance matrix
FloydWarshall(int vertices) : n(vertices) {
dist.resize(n, vector<int>(n, INT_MAX)); // Resize the matrix with INT_MAX initially
}
// Method to take input for the adjacency matrix
void inputGraph() {
cout << "Enter the adjacency matrix (use 0 for no direct edge and other positive values for edge weights):\n";
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> dist[i][j];
if (dist[i][j] == 0 && i != j) {
dist[i][j] = INT_MAX; // No path exists, set to infinity
}
}
}
}
// Method to implement the Floyd-Warshall algorithm
void runAlgorithm() {
// Loop over each intermediate node (k)
for (int k = 0; k < n; k++) {
// Loop over each source node (i)
for (int i = 0; i < n; i++) {
// Loop over each destination node (j)
for (int j = 0; j < n; j++) {
// If a shorter path is found through the intermediate node k
if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
}
// Method to print the distance matrix
void printSolution() {
cout << "The shortest distances between every pair of vertices are:\n";
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][j] == INT_MAX) {
cout << "INF "; // If no path exists, print INF
} else {
cout << dist[i][j] << " ";
}
}
cout << endl;
}
}
};
int main() {
int n;
// Take input for number of vertices in the graph
cout << "Enter the number of vertices: ";
cin >> n;
// Create an object of FloydWarshall class
FloydWarshall fw(n);
// Take input for the adjacency matrix
fw.inputGraph();
// Run the Floyd-Warshall algorithm
fw.runAlgorithm();
// Print the result (shortest distances)
fw.printSolution();
return 0;
}
Enter the number of vertices: 4
Enter the adjacency matrix (use 0 for no direct edge and other positive values for edge weights):
0 3 0 0
3 0 4 0
0 4 0 2
0 0 2 0
The shortest distances between every pair of vertices are:
0 3 7 5
3 0 4 6
7 4 0 2
5 6 2 0 Networks Flow : Bipartite Matching

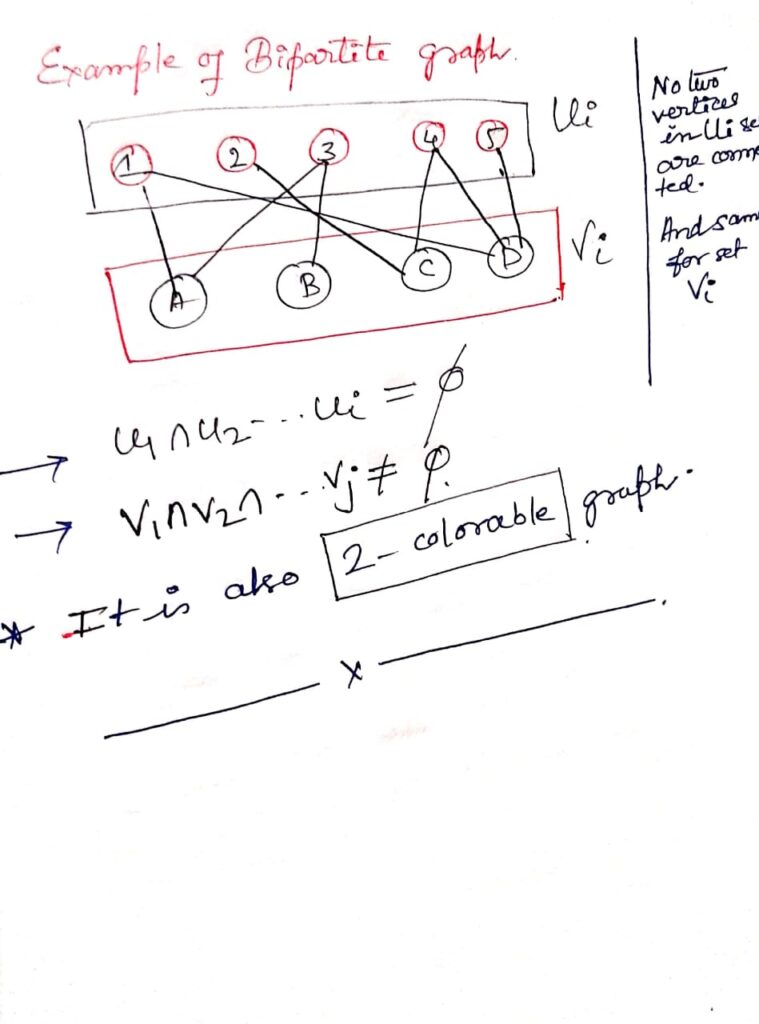
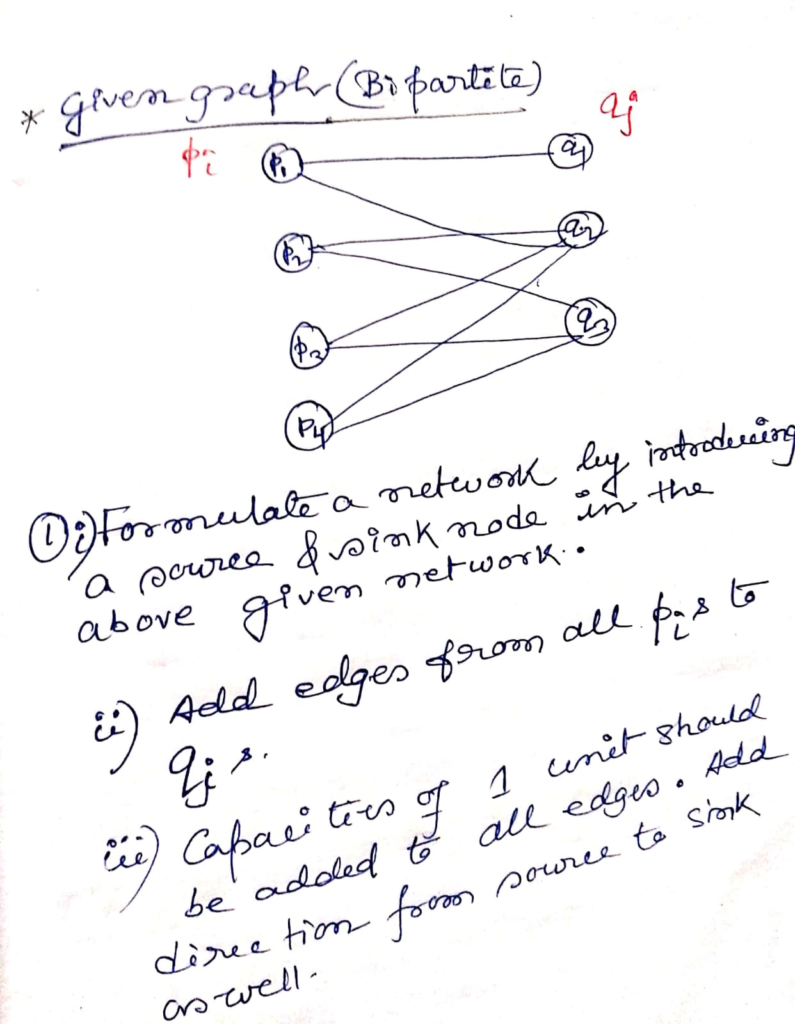
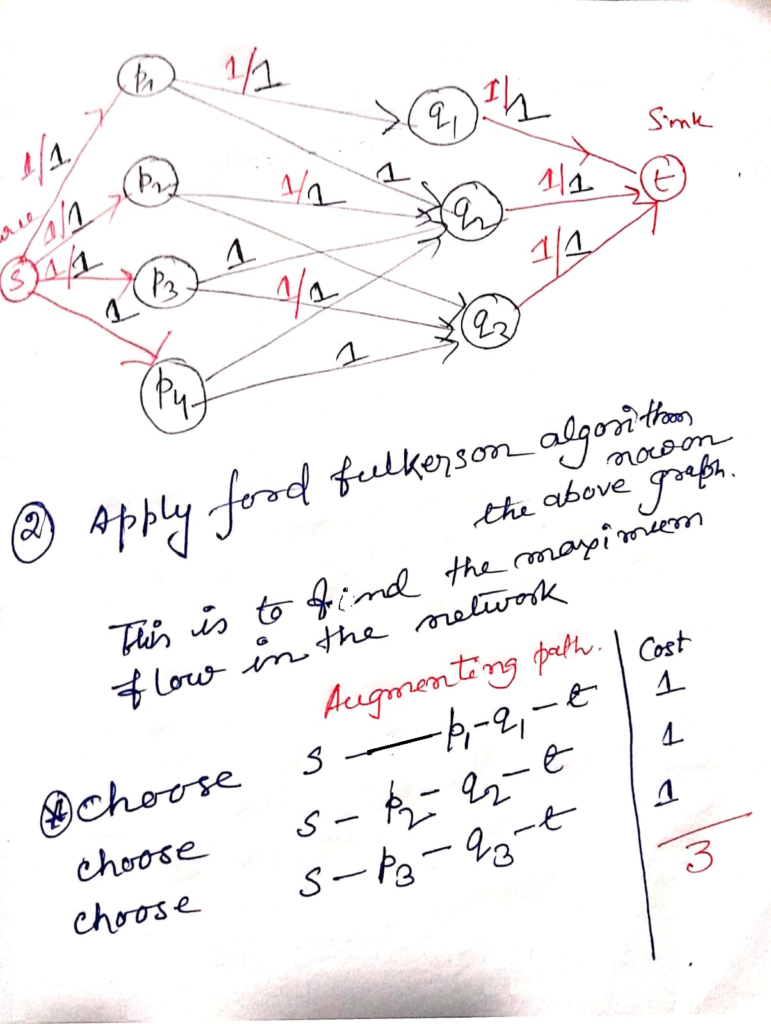
// C code for bipartite matching
#include <stdio.h>
#include <stdbool.h>
// Function to check if a path exists from u to v using BFS
bool bpm(bool bpGraph[100][100], int u, bool seen[], int matchR[]) {
// Base case: If this column is not assigned to any row yet
for (int v = 0; v < 100; v++) {
if (bpGraph[u][v] && !seen[v]) {
seen[v] = true;
// If v is not visited and there is an edge from u to v,
// then try to assign this v to an unmatched row.
if (matchR[v] < 0 || bpm(bpGraph, matchR[v], seen, matchR)) {
matchR[v] = u;
return true;
}
}
}
return false;
}
// Returns maximum number of matching from M to N
int maxBPM(bool bpGraph[100][100], int n) {
// An array to keep track of the matchings of the vertices of N
int matchR[100];
// Initially all jobs are available
for(int i = 0; i < 100; i++)
matchR[i] = -1;
int result = 0; // Count of jobs assigned to applicants
for (int u = 0; u < n; u++) {
// Mark all vertices as not visited for next applicant.
bool seen[100];
for(int i=0; i<100; i++)
seen[i] = false;
// Find if the applicant 'u' can get any job
if (bpm(bpGraph, u, seen, matchR))
result++;
}
return result;
}
// Driver code
int main() {
// Let us create a sample graph
// where the applicants are at one side of the
// graph, jobs at the other side and connecting
// lines indicate possible assignments.
bool bpGraph[100][100] = {
{0, 1, 1, 0, 0},
{1, 0, 0, 1, 0},
{0, 0, 1, 0, 1},
{0, 0, 0, 0, 0},
{0, 0, 1, 0, 1}
};
int n = 5;
printf("Maximum number of applicants that can be assigned jobs = %d\n", maxBPM(bpGraph, n));
return 0;
}
Output :
Maximum number of applicants that can be assigned jobs = 3// C++ code for bipartite matching
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
class BipartiteMatching {
private:
int N; // Number of vertices on the left side
int M; // Number of vertices on the right side
vector<vector<int>> graph;
public:
BipartiteMatching(int N, int M) {
this->N = N;
this->M = M;
graph.resize(N, vector<int>(M, 0));
}
void addEdge(int u, int v) {
graph[u][v] = 1;
}
bool bfs(vector<int>& matchR, vector<bool>& seen) {
queue<int> q;
for (int u = 0; u < N; u++) {
if (matchR[u] == -1) {
seen[u] = true;
q.push(u);
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v = 0; v < M; v++) {
if (graph[u][v] && !seen[v]) {
seen[v] = true;
if (matchR[v] < 0 || bfs(matchR, seen)) {
matchR[v] = u;
return true;
}
}
}
}
return false;
}
int maxMatching() {
vector<int> matchR(M, -1); // Array to store the matchings
int result = 0;
for (int u = 0; u < N; u++) {
vector<bool> seen(M, false);
if (bfs(matchR, seen)) {
result++;
}
}
return result;
}
};
int main() {
int N = 5, M = 5;
BipartiteMatching bm(N, M);
bm.addEdge(0, 1);
bm.addEdge(0, 2);
bm.addEdge(1, 0);
bm.addEdge(1, 3);
bm.addEdge(2, 2);
bm.addEdge(2, 4);
bm.addEdge(4, 2);
bm.addEdge(4, 4);
cout << "Maximum number of matchings: " << bm.maxMatching() << endl;
return 0;
}
Output :
Maximum number of applicants that can be assigned jobs = 3Explanation:
- Include Headers:
iostream: For input/output operations.vector: For using thevectorSTL.queue: For using thequeueSTL in the BFS implementation.
- BipartiteMatching Class:
- Private Members:
N: Number of vertices on the left side.M: Number of vertices on the right side.graph: A 2D vector representing the bipartite graph.graph[u][v]is 1 if there’s an edge fromutov, 0 otherwise.
- Public Members:
- Constructor: Initializes
N,M, and resizes thegraphvector. - addEdge(): Adds an edge between vertices
uandv. - bfs(): Implements Breadth-First Search to find an augmenting path.
- maxMatching(): Finds the maximum number of matchings in the bipartite graph.
- Constructor: Initializes
- Private Members:
- bfs() Function:
- Uses a queue to perform BFS.
- Initially, enqueues all unmatched vertices on the left side.
- In each iteration:
- Dequeues a vertex
u. - Explores all neighbors
vofu. - If
vis not visited:- Marks
vas visited. - If
vis unmatched or an augmenting path can be found for the vertex currently matched withv, assignutovand returntrue.
- Marks
- Dequeues a vertex
- maxMatching() Function:
- Initializes an array
matchRto store the matchings. - Iterates through all vertices on the left side.
- Calls
bfs()to check if an augmenting path exists for the current vertex. - If an augmenting path is found, increment the
resultcount.
- Calls
- Returns the maximum number of matchings.
- Initializes an array
- main() Function:
- Creates a
BipartiteMatchingobject. - Adds edges to the graph using
addEdge(). - Calls
maxMatching()to find the maximum number of matchings. - Prints the result.
- Creates a
This above C++ code provides a more object-oriented and concise implementation of the bipartite matching algorithm using STL features like vector and queue.
Cycle Cancellation Algorithm
Dijkstra algorithm
// C code for Dijkstra algorithm
#include <stdio.h>
#include <limits.h>
#define V 9 // Number of vertices in the graph
// Function to print the constructed distance array
void printSolution(int dist[])
{
printf("Vertex \t\t Distance from Source\n");
for (int i = 0; i < V; i++)
printf("%d \t\t %d\n", i, dist[i]);
}
// Function to find the vertex with the minimum distance value,
// from the set of vertices not yet included in shortest path tree
int minDistance(int dist[], bool sptSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
// Function to implement Dijkstra's single source shortest path algorithm
// from a given source to all other vertices
void dijkstra(int graph[V][V], int src)
{
int dist[V]; // The output array. dist[i] will hold the shortest
// distance from src to i
bool sptSet[V]; // sptSet[i] will be true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
// Initialize all distances as INFINITE and stptSet[] as false
for (int i = 0; i < V; i++)
dist[i] = INT_MAX, sptSet[i] = false;
// Distance of source vertex from itself will always be 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of vertices
// not yet processed. u is always equal to src in the first iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an edge from
// u to v, and total weight of path from src to v through u is
// smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist);
}
// Driver program to test above functions
int main()
{
/* Let us create the example graph discussed above */
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}
Output:
Vertex Distance from Source
0 0
1 4
2 8
3 7
4 9
5 10
6 2
7 8
8 7
This output shows the shortest distances from vertex 0 to all other vertices in the given grap//C++ code for Dijkstra algorithm
#include <iostream>
#include <vector>
#include <limits.h>
#include <algorithm>
using namespace std;
class Graph {
private:
int V; // Number of vertices
vector<vector<int>> adj; // Adjacency list representation
public:
Graph(int V) {
this->V = V;
adj.resize(V);
}
void addEdge(int u, int v, int w) {
adj[u].push_back({v, w});
// Assuming undirected graph, add edge in both directions
adj[v].push_back({u, w});
}
int minDistance(vector<int>& dist, vector<bool>& sptSet) {
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min)
min = dist[v], min_index = v;
return min_index;
}
void dijkstra(int src) {
vector<int> dist(V, INT_MAX);
vector<bool> sptSet(V, false);
dist[src] = 0;
for (int count = 0; count < V - 1; count++) {
int u = minDistance(dist, sptSet);
sptSet[u] = true;
for (auto i : adj[u]) {
int v = i[0];
int weight = i[1];
if (!sptSet[v] && dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
cout << "Vertex \t\t Distance from Source\n";
for (int i = 0; i < V; i++)
cout << i << " \t\t " << dist[i] << endl;
}
};
int main() {
int V = 9;
Graph g(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
g.dijkstra(0);
return 0;
}