- How does the branch and bound method work?
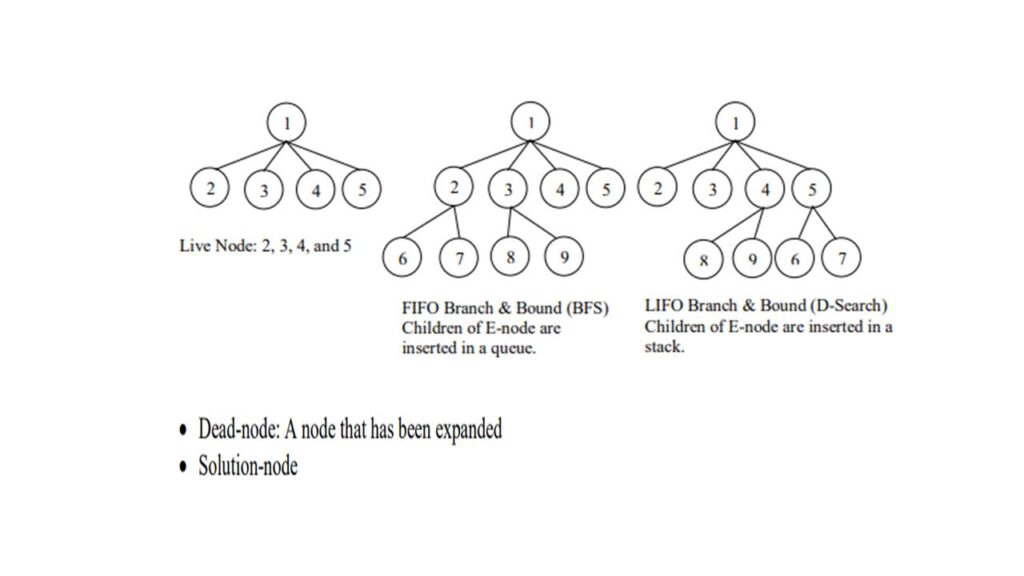
- Live node, e-node, and dead node
- FIFO-BB and LIFO-BB
- Job Sequencing with Deadlines using Branch and Bound.
- How does it work (FIFOBB for Job Sequencing)?
- Branch and bound solution for 0-1 knapsack problem
- Branch and bound solution for Travelling Sales Person (TSP) problem
- Branch and bound solution for N-Queen problem
- Explanation of NQUEEN, Knapsack & Job Assignment solution using Branch and Bound
- Least cost branch and bound (LC-BB)
- A* algorithm is LC-BB



Job Sequencing with Deadlines using Branch and Bound.
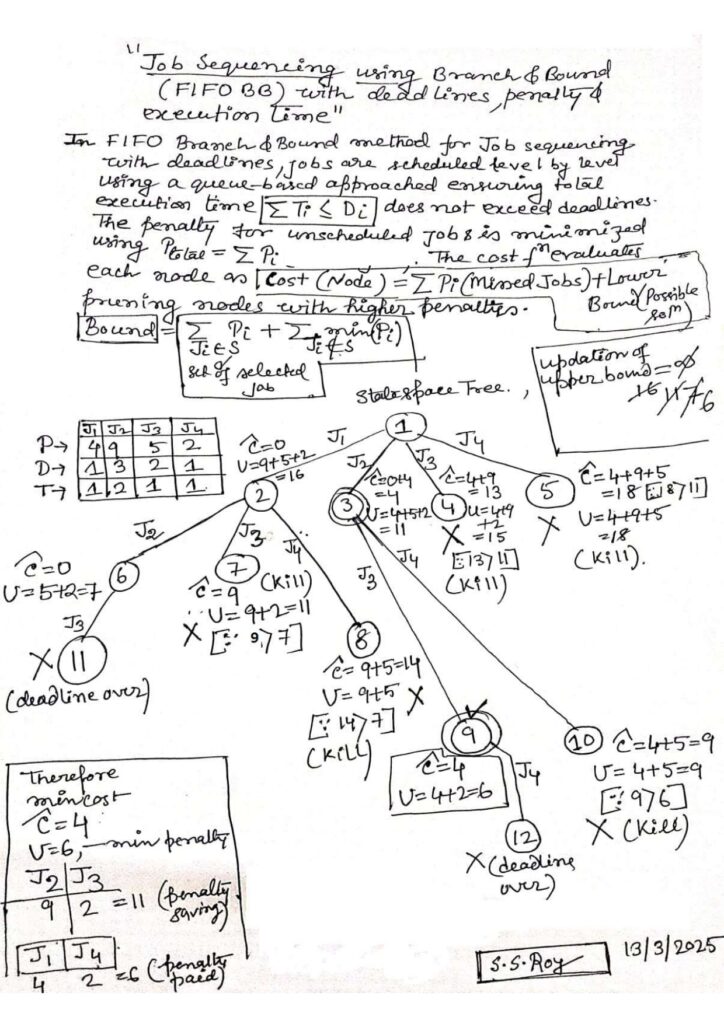
How does FIFO BB work for job sequencing with deadlines, penalties, and execution time?
Solving 0-1 Knapsack using Branch and Bound
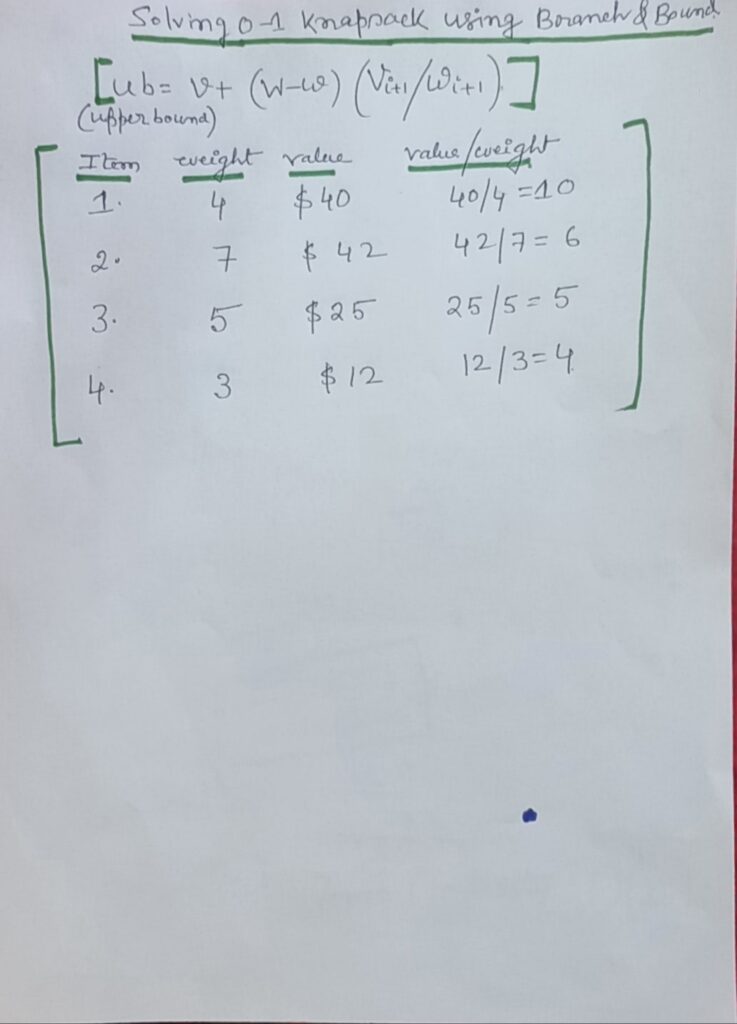
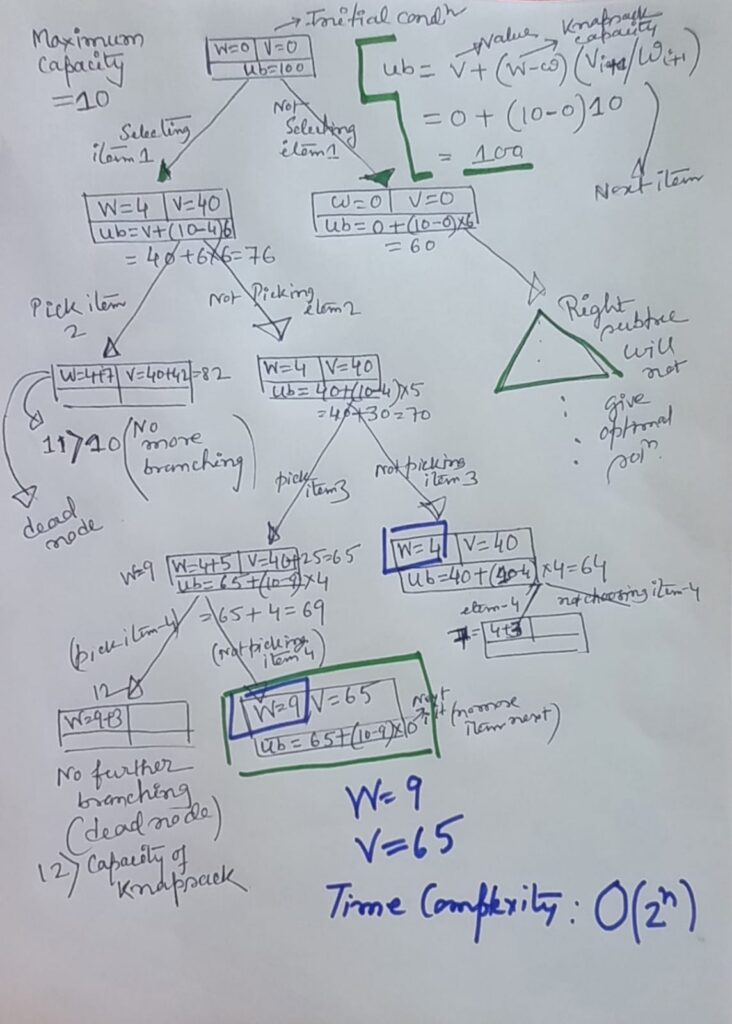
// C code for solving 0-1 Knapsack using Branch and Bound
#include <stdio.h>
#include <stdlib.h>
// Structure to store the item information
typedef struct {
int weight; // Weight of the item
int value; // Value of the item
float ratio; // Value-to-weight ratio of the item (used for sorting)
} Item;
// Structure to store the state of the node in the search tree
typedef struct {
int level; // The current level of the node (which item is being considered)
int profit; // The current profit obtained by including/excluding items
int weight; // The total weight of the items included so far
float bound; // The upper bound of the profit that can be achieved from this node
} Node;
// Function to calculate the bound (upper bound) for a node in the search tree
float bound(Node u, int n, int W, Item items[]) {
// If the current node's weight is more than the capacity, return 0 (no profit)
if (u.weight >= W) return 0;
// Initialize the result as the profit of the current node
float result = u.profit;
// Start from the next item in the list
int j = u.level + 1;
int totalWeight = u.weight;
// Include items greedily until the knapsack is full or we run out of items
while (j < n && totalWeight + items[j].weight <= W) {
totalWeight += items[j].weight; // Add the item to the knapsack
result += items[j].value; // Add the value of the item
j++; // Move to the next item
}
// If there are still items left, take the fractional part of the next item (fractional knapsack)
if (j < n) {
result += (W - totalWeight) * items[j].ratio; // Add fraction of the next item
}
return result; // Return the upper bound for the current node
}
// Comparison function to sort items based on their value-to-weight ratio (descending order)
int compare(const void *a, const void *b) {
// Cast the void pointers to Item pointers to access their value-to-weight ratio
float r1 = ((Item*)a)->ratio;
float r2 = ((Item*)b)->ratio;
// Compare the ratios in descending order
return (r1 < r2) - (r1 > r2); // Return 1 if r1 < r2, -1 if r1 > r2, 0 if equal
}
// Function to solve the Knapsack problem using Branch and Bound
int knapsack(int n, int W, Item items[]) {
// Calculate value-to-weight ratio for each item
for (int i = 0; i < n; i++) {
items[i].ratio = (float)items[i].value / items[i].weight; // Value per unit weight
}
// Sort the items based on value-to-weight ratio in descending order
qsort(items, n, sizeof(Item), compare);
// Initialize the root node with no items considered yet
Node u, v;
u.level = -1; // Start at level -1 (no item considered yet)
u.profit = 0; // No profit initially
u.weight = 0; // No weight initially
u.bound = bound(u, n, W, items); // Calculate the upper bound of profit at the root
// Create a queue for BFS-like traversal of the search tree (node processing)
Node queue[1000];
int front = 0, rear = 0; // Initialize the queue (front and rear pointers)
queue[rear++] = u; // Add the root node to the queue
int maxProfit = 0; // Variable to store the maximum profit found so far
// Process nodes in the queue until the queue is empty
while (front != rear) {
u = queue[front++]; // Get the next node from the queue
// If the upper bound of the current node is less than the best solution found, prune the node
if (u.bound <= maxProfit) continue;
// Case 1: Include the next item (item at level u.level + 1)
v.level = u.level + 1; // Move to the next level in the decision tree
v.weight = u.weight + items[v.level].weight; // Add the weight of the next item
v.profit = u.profit + items[v.level].value; // Add the value of the next item
// If the new node is valid (does not exceed the knapsack capacity) and improves the solution, update maxProfit
if (v.weight <= W && v.profit > maxProfit) {
maxProfit = v.profit; // Update the maximum profit
}
// Calculate the upper bound for the "include" branch
v.bound = bound(v, n, W, items);
// If the bound for this branch is greater than the best known solution, add it to the queue
if (v.bound > maxProfit) {
queue[rear++] = v; // Add this node to the queue
}
// Case 2: Exclude the next item (move to the next level without including the item)
v.weight = u.weight; // Do not include the weight of the next item
v.profit = u.profit; // Do not add the value of the next item
// Calculate the upper bound for the "exclude" branch
v.bound = bound(v, n, W, items);
// If the bound for this branch is greater than the best known solution, add it to the queue
if (v.bound > maxProfit) {
queue[rear++] = v; // Add this node to the queue
}
}
return maxProfit; // Return the maximum profit found
}
int main() {
int n, W;
// Input the number of items and the capacity of the knapsack
printf("Enter the number of items: ");
scanf("%d", &n);
printf("Enter the capacity of the knapsack: ");
scanf("%d", &W);
// Declare an array to store the items
Item items[n];
// Input the weight and value of each item
printf("Enter the weight and value of each item:\n");
for (int i = 0; i < n; i++) {
scanf("%d %d", &items[i].weight, &items[i].value);
}
// Call the knapsack function using Branch and Bound to find the maximum profit
int maxProfit = knapsack(n, W, items);
// Output the maximum value that can be obtained with the given capacity
printf("The maximum value that can be obtained is: %d\n", maxProfit);
return 0; // Return 0 to indicate successful program execution
}
Output :
Enter the number of items: 4
Enter the capacity of the knapsack: 50
Enter the weight and value of each item:
10 60
20 100
30 110
12 14
The maximum value that can be obtained is: 210
Process returned 0 (0x0) execution time : 59.469 s
Press any key to continue.
//Track which items are included in the optimal solution.
//Display the items picked at the end.
#include <stdio.h>
#include <stdlib.h>
// Structure to store the item information
typedef struct {
int weight; // Weight of the item
int value; // Value of the item
float ratio; // Value-to-weight ratio of the item (used for sorting)
} Item;
// Structure to store the state of the node in the search tree
typedef struct {
int level; // The current level of the node (which item is being considered)
int profit; // The current profit obtained by including/excluding items
int weight; // The total weight of the items included so far
float bound; // The upper bound of the profit that can be achieved from this node
int *included; // Array to track the items included in the knapsack at this node
} Node;
// Function to calculate the bound (upper bound) for a node in the search tree
float bound(Node u, int n, int W, Item items[]) {
// If the current node's weight is more than the capacity, return 0 (no profit)
if (u.weight >= W) return 0;
// Initialize the result as the profit of the current node
float result = u.profit;
// Start from the next item in the list
int j = u.level + 1;
int totalWeight = u.weight;
// Include items greedily until the knapsack is full or we run out of items
while (j < n && totalWeight + items[j].weight <= W) {
totalWeight += items[j].weight; // Add the item to the knapsack
result += items[j].value; // Add the value of the item
j++; // Move to the next item
}
// If there are still items left, take the fractional part of the next item (fractional knapsack)
if (j < n) {
result += (W - totalWeight) * items[j].ratio; // Add fraction of the next item
}
return result; // Return the upper bound for the current node
}
// Comparison function to sort items based on their value-to-weight ratio (descending order)
int compare(const void *a, const void *b) {
// Cast the void pointers to Item pointers to access their value-to-weight ratio
float r1 = ((Item*)a)->ratio;
float r2 = ((Item*)b)->ratio;
// Compare the ratios in descending order
return (r1 < r2) - (r1 > r2); // Return 1 if r1 < r2, -1 if r1 > r2, 0 if equal
}
// Function to solve the Knapsack problem using Branch and Bound
int knapsack(int n, int W, Item items[]) {
// Calculate value-to-weight ratio for each item
for (int i = 0; i < n; i++) {
items[i].ratio = (float)items[i].value / items[i].weight; // Value per unit weight
}
// Sort the items based on value-to-weight ratio in descending order
qsort(items, n, sizeof(Item), compare);
// Initialize the root node with no items considered yet
Node u, v;
u.level = -1; // Start at level -1 (no item considered yet)
u.profit = 0; // No profit initially
u.weight = 0; // No weight initially
u.bound = bound(u, n, W, items); // Calculate the upper bound of profit at the root
u.included = (int*)calloc(n, sizeof(int)); // Allocate memory to track included items
// Create a queue for BFS-like traversal of the search tree (node processing)
Node queue[1000];
int front = 0, rear = 0; // Initialize the queue (front and rear pointers)
queue[rear++] = u; // Add the root node to the queue
int maxProfit = 0; // Variable to store the maximum profit found so far
Node bestSolution; // Store the best solution (with selected items)
// Process nodes in the queue until the queue is empty
while (front != rear) {
u = queue[front++]; // Get the next node from the queue
// If the upper bound of the current node is less than the best solution found, prune the node
if (u.bound <= maxProfit) continue;
// Case 1: Include the next item (item at level u.level + 1)
v.level = u.level + 1; // Move to the next level in the decision tree
v.weight = u.weight + items[v.level].weight; // Add the weight of the next item
v.profit = u.profit + items[v.level].value; // Add the value of the next item
v.included = (int*)malloc(n * sizeof(int)); // Allocate memory for included items
memcpy(v.included, u.included, n * sizeof(int)); // Copy the inclusion array
// Mark the item as included
v.included[v.level] = 1;
// If the new node is valid (does not exceed the knapsack capacity) and improves the solution, update maxProfit
if (v.weight <= W && v.profit > maxProfit) {
maxProfit = v.profit; // Update the maximum profit
bestSolution = v; // Store the best solution found so far
}
// Calculate the upper bound for the "include" branch
v.bound = bound(v, n, W, items);
// If the bound for this branch is greater than the best known solution, add it to the queue
if (v.bound > maxProfit) {
queue[rear++] = v; // Add this node to the queue
}
// Case 2: Exclude the next item (move to the next level without including the item)
v.weight = u.weight; // Do not include the weight of the next item
v.profit = u.profit; // Do not add the value of the next item
v.included = (int*)malloc(n * sizeof(int)); // Allocate memory for included items
memcpy(v.included, u.included, n * sizeof(int)); // Copy the inclusion array
// Mark the item as excluded
v.included[v.level] = 0;
// Calculate the upper bound for the "exclude" branch
v.bound = bound(v, n, W, items);
// If the bound for this branch is greater than the best known solution, add it to the queue
if (v.bound > maxProfit) {
queue[rear++] = v; // Add this node to the queue
}
}
// Return the maximum profit found and the best solution
// Output the selected items
printf("\nItems included in the knapsack:\n");
for (int i = 0; i < n; i++) {
if (bestSolution.included[i]) {
printf("Item %d (Weight: %d, Value: %d)\n", i+1, items[i].weight, items[i].value);
}
}
// Clean up allocated memory
free(u.included);
free(bestSolution.included);
return maxProfit; // Return the maximum profit found
}
int main() {
int n, W;
// Input the number of items and the capacity of the knapsack
printf("Enter the number of items: ");
scanf("%d", &n);
printf("Enter the capacity of the knapsack: ");
scanf("%d", &W);
// Declare an array to store the items
Item items[n];
// Input the weight and value of each item
printf("Enter the weight and value of each item:\n");
for (int i = 0; i < n; i++) {
scanf("%d %d", &items[i].weight, &items[i].value);
}
// Call the knapsack function using Branch and Bound to find the maximum profit
int maxProfit = knapsack(n, W, items);
// Output the maximum value that can be obtained with the given capacity
printf("\nThe maximum value that can be obtained is: %d\n", maxProfit);
return 0; // Return 0 to indicate successful program execution
}//C++ code WITH STRUCTURE
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
// Structure to represent an item with its weight, value, and value-to-weight ratio
struct Item {
int weight;
int value;
float ratio; // Value-to-weight ratio
};
// Structure to represent a node in the search tree
struct Node {
int level; // Current level (which item is being considered)
int profit; // Current profit obtained
int weight; // Current total weight
float bound; // Upper bound on the profit achievable from this node
};
// Function to calculate the upper bound for a node
float bound(Node u, int n, int W, Item items[]) {
// If the current weight exceeds the knapsack capacity, no profit is possible
if (u.weight >= W)
return 0;
float result = u.profit;
int j = u.level + 1;
int totalWeight = u.weight;
// Greedily include items until the knapsack is full or all items are considered
while (j < n && totalWeight + items[j].weight <= W) {
totalWeight += items[j].weight;
result += items[j].value;
j++;
}
// If there's still space in the knapsack, include a fraction of the next item
if (j < n) {
result += (W - totalWeight) * items[j].ratio;
}
return result;
}
// Comparison function to sort items by their value-to-weight ratio in descending order
bool compare(Item a, Item b) {
return a.ratio > b.ratio;
}
// Function to solve the Knapsack problem using Branch and Bound
int knapsack(int n, int W, Item items[]) {
// Calculate value-to-weight ratio for each item
for (int i = 0; i < n; i++) {
items[i].ratio = (float)items[i].value / items[i].weight;
}
// Sort items in descending order of their value-to-weight ratio
sort(items, items + n, compare);
// Initialize the root node
Node u, v;
u.level = -1;
u.profit = 0;
u.weight = 0;
u.bound = bound(u, n, W, items);
// Create a queue to perform BFS-like traversal of the search tree
queue<Node> q;
q.push(u);
int maxProfit = 0; // To store the maximum profit found so far
// Process nodes in the queue until it becomes empty
while (!q.empty()) {
u = q.front();
q.pop();
// Prune the node if its upper bound is less than or equal to the current best profit
if (u.bound <= maxProfit)
continue;
// Case 1: Include the next item
v.level = u.level + 1;
v.weight = u.weight + items[v.level].weight;
v.profit = u.profit + items[v.level].value;
// If the new node is feasible and has a better profit, update the maximum profit
if (v.weight <= W && v.profit > maxProfit) {
maxProfit = v.profit;
}
// Calculate the upper bound for the "include" branch
v.bound = bound(v, n, W, items);
// Add the "include" node to the queue if its bound is promising
if (v.bound > maxProfit) {
q.push(v);
}
// Case 2: Exclude the next item
v.weight = u.weight;
v.profit = u.profit;
// Calculate the upper bound for the "exclude" branch
v.bound = bound(v, n, W, items);
// Add the "exclude" node to the queue if its bound is promising
if (v.bound > maxProfit) {
q.push(v);
}
}
return maxProfit;
}
int main() {
int n, W;
cout << "Enter the number of items: ";
cin >> n;
cout << "Enter the capacity of the knapsack: ";
cin >> W;
Item items[n];
cout << "Enter the weight and value of each item:\n";
for (int i = 0; i < n; i++) {
cin >> items[i].weight >> items[i].value;
}
int maxProfit = knapsack(n, W, items);
cout << "The maximum value that can be obtained is: " << maxProfit << endl;
return 0;
}
Enter the number of items: 3
Enter the capacity of the knapsack: 10
Enter the weight and value of each item:
2 4
5 5
3 6
The maximum value that can be obtained is: 15
Process returned 0 (0x0) execution time : 31.722 s
Press any key to continue.
//C++ code with class and vector STL
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
// Class to represent an item with its weight, value, and value-to-weight ratio
class Item {
public:
int weight;
int value;
float ratio; // Value-to-weight ratio
Item(int w, int v) : weight(w), value(v), ratio((float)v / w) {}
};
// Structure to represent a node in the search tree
struct Node {
int level; // Current level (which item is being considered)
int profit; // Current profit obtained
int weight; // Current total weight
float bound; // Upper bound on the profit achievable from this node
};
// Function to calculate the upper bound for a node
float bound(Node u, int n, int W, const vector<Item>& items) {
if (u.weight >= W)
return 0;
float result = u.profit;
int j = u.level + 1;
int totalWeight = u.weight;
while (j < n && totalWeight + items[j].weight <= W) {
totalWeight += items[j].weight;
result += items[j].value;
j++;
}
if (j < n) {
result += (W - totalWeight) * items[j].ratio;
}
return result;
}
// Comparison function to sort items by their value-to-weight ratio in descending order
bool compare(const Item& a, const Item& b) {
return a.ratio > b.ratio;
}
// Function to solve the Knapsack problem using Branch and Bound
int knapsack(int n, int W, const vector<Item>& items) {
// Sort items in descending order of their value-to-weight ratio
sort(items.begin(), items.end(), compare);
// Initialize the root node
Node u, v;
u.level = -1;
u.profit = 0;
u.weight = 0;
u.bound = bound(u, n, W, items);
// Create a queue to perform BFS-like traversal of the search tree
queue<Node> q;
q.push(u);
int maxProfit = 0; // To store the maximum profit found so far
// Process nodes in the queue until it becomes empty
while (!q.empty()) {
u = q.front();
q.pop();
// Prune the node if its upper bound is less than or equal to the current best profit
if (u.bound <= maxProfit)
continue;
// Case 1: Include the next item
v.level = u.level + 1;
v.weight = u.weight + items[v.level].weight;
v.profit = u.profit + items[v.level].value;
// If the new node is feasible and has a better profit, update the maximum profit
if (v.weight <= W && v.profit > maxProfit) {
maxProfit = v.profit;
}
// Calculate the upper bound for the "include" branch
v.bound = bound(v, n, W, items);
// Add the "include" node to the queue if its bound is promising
if (v.bound > maxProfit) {
q.push(v);
}
// Case 2: Exclude the next item
v.weight = u.weight;
v.profit = u.profit;
// Calculate the upper bound for the "exclude" branch
v.bound = bound(v, n, W, items);
// Add the "exclude" node to the queue if its bound is promising
if (v.bound > maxProfit) {
q.push(v);
}
}
return maxProfit;
}
int main() {
int n, W;
cout << "Enter the number of items: ";
cin >> n;
cout << "Enter the capacity of the knapsack: ";
cin >> W;
vector<Item> items;
cout << "Enter the weight and value of each item:\n";
for (int i = 0; i < n; i++) {
int w, v;
cin >> w >> v;
items.push_back(Item(w, v));
}
int maxProfit = knapsack(n, W, items);
cout << "The maximum value that can be obtained is: " << maxProfit << endl;
return 0;
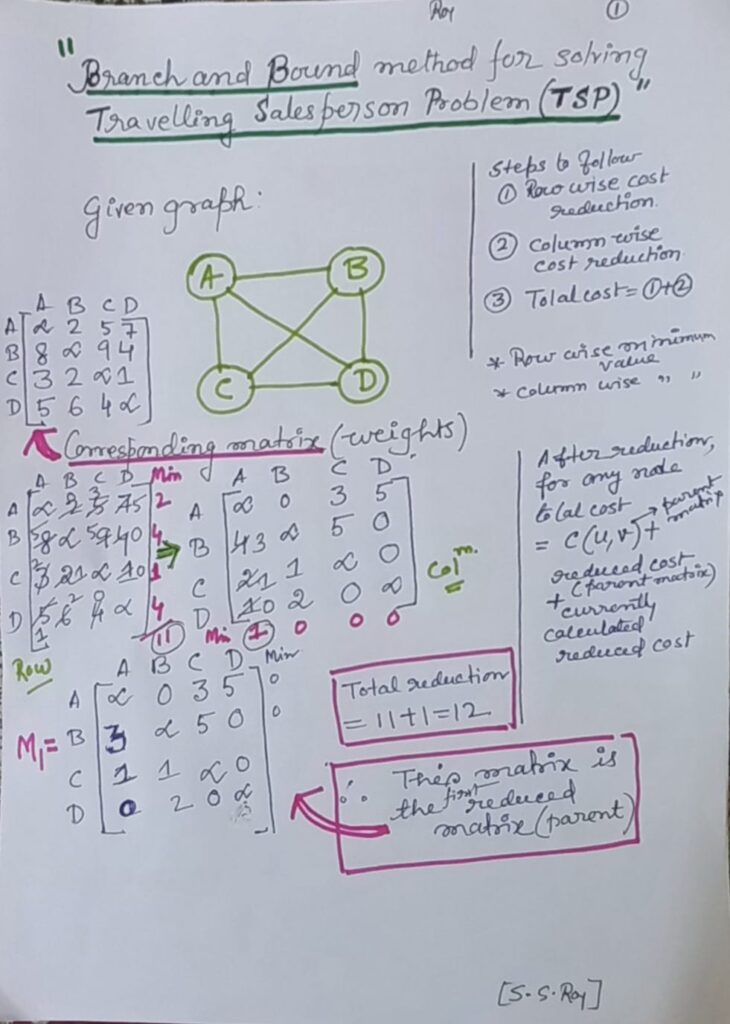
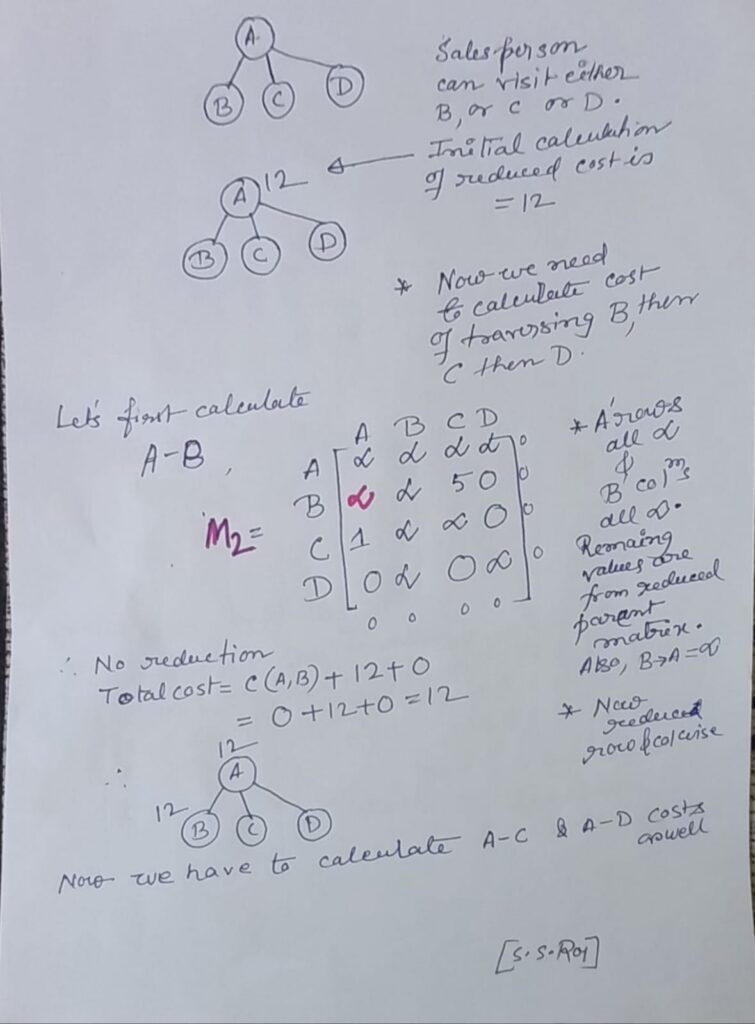
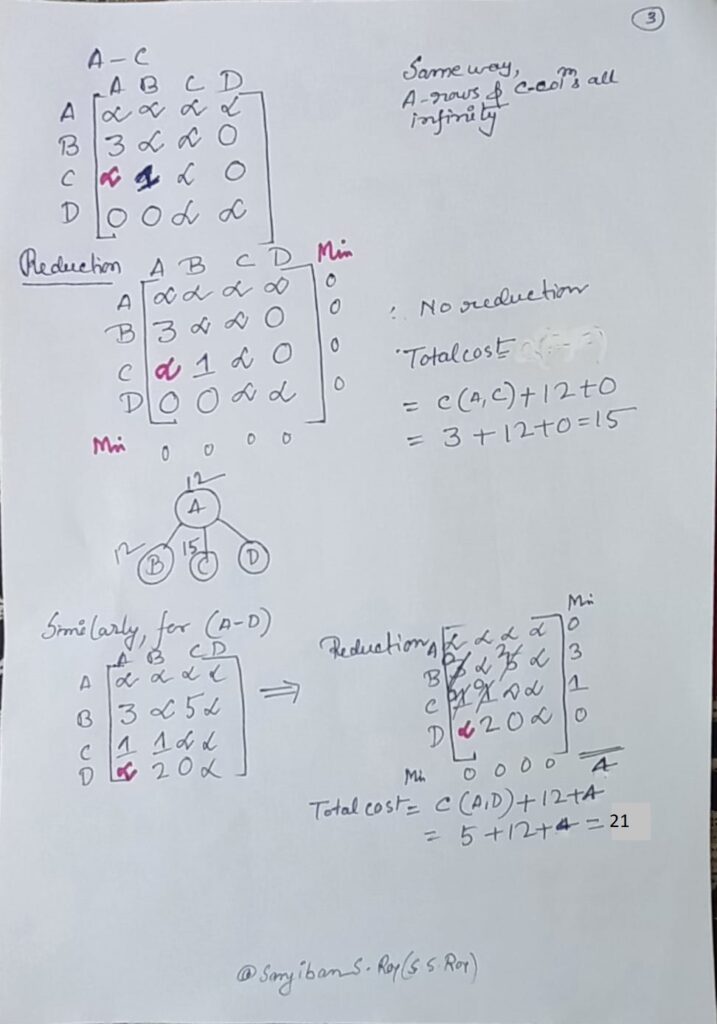
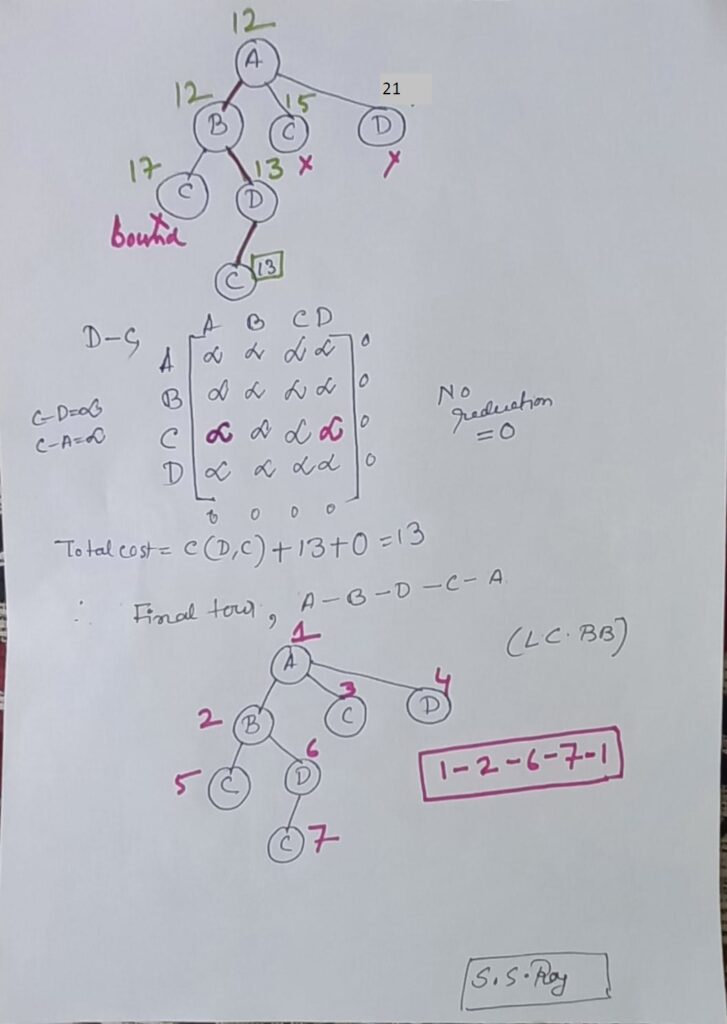
}Branch and bound for Travelling Sales Person (TSP) problem
The travelling salesperson problem, also known as travelling salesman problem (TSP), asks the following question: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?” It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
The travelling purchaser problem and the vehicle routing problem are both generalizations of TSP.

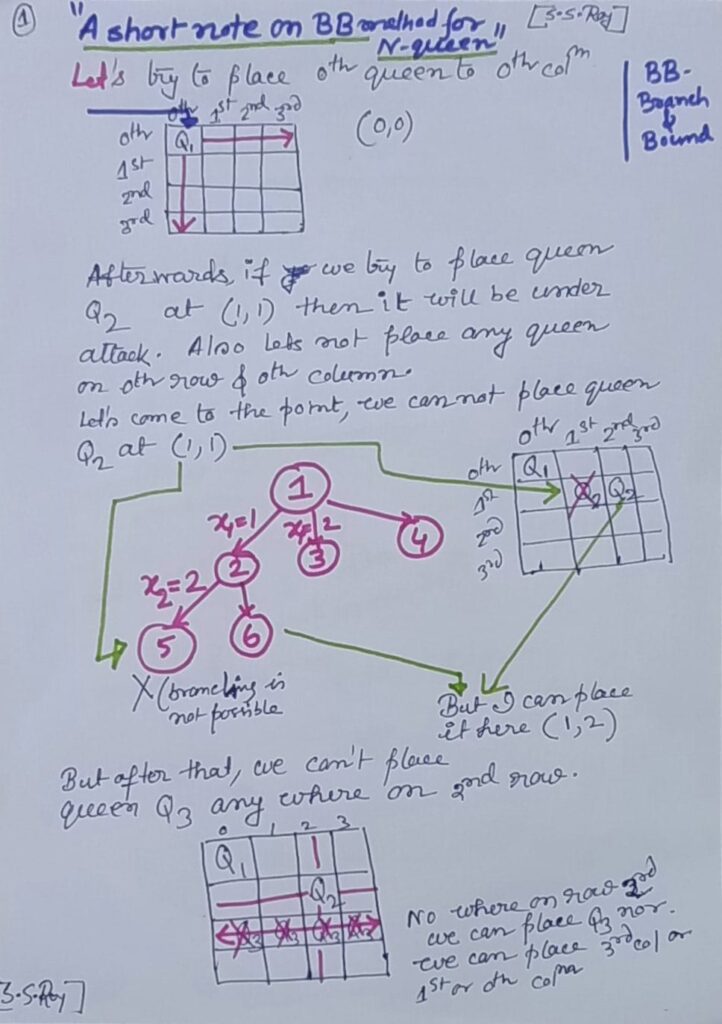
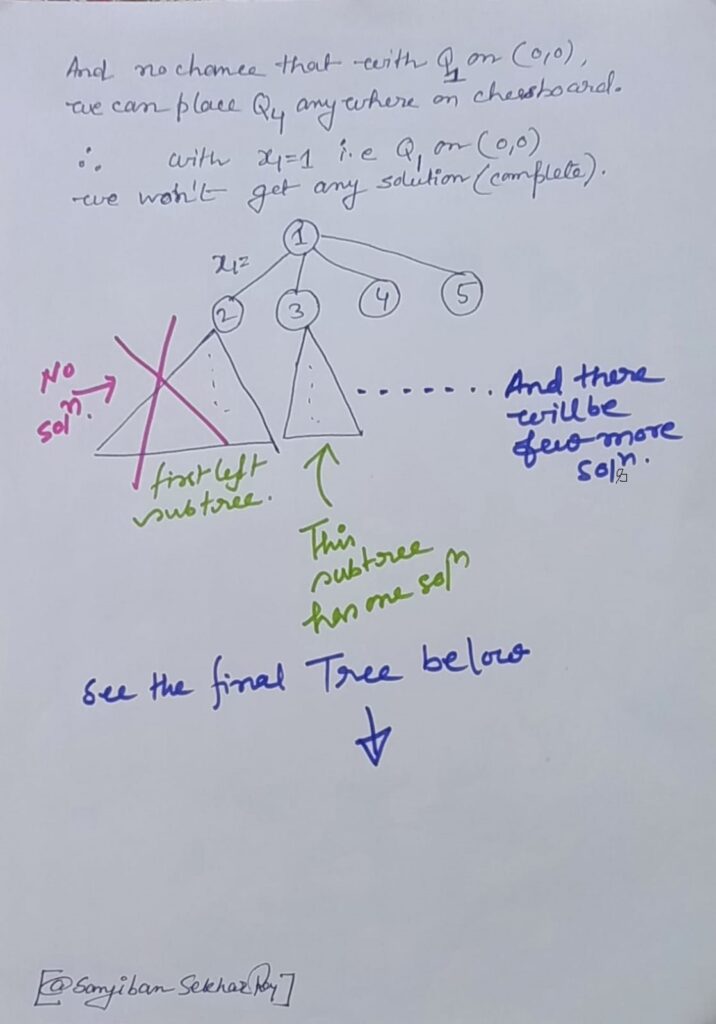
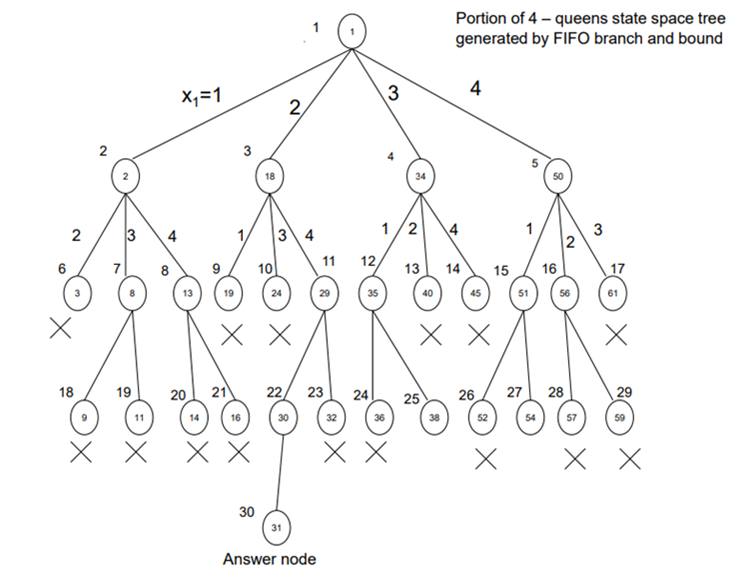
Solving 4 queen problem using Branch and Bound
Imagine a game of chess where you’re tasked with placing queens on a chessboard. The catch? You can’t place them where they’ll threaten each other. This puzzle is known as the N Queens problem, where you have to position N queens on an N×N chessboard without any of them being able to attack each other. So, no sharing rows, columns, or diagonals!
Now, let’s talk about two ways to tackle this challenge: backtracking and Branch and Bound.
In the backtracking method, you start by placing queens one by one, column by column. When you place a queen in a column, you check if it clashes with any previously placed queens. If it does, you backtrack and try another spot. Simple, right?
Now, Branch and Bound takes a slightly different approach. It’s like peeking ahead in a maze.
//C code for TSP
#include <stdio.h>
#include <limits.h>
#define MAX_CITIES 20
int dist[MAX_CITIES][MAX_CITIES]; // Matrix to store distances between cities
int visited[MAX_CITIES]; // Array to keep track of visited cities
int min_cost = INT_MAX; // Minimum cost of the tour
// Function to calculate the lower bound for a given path
int lower_bound(int city) {
int i, j;
int lb = 0;
for (i = 0; i < MAX_CITIES; i++) {
if (!visited[i]) {
int min = INT_MAX;
for (j = 0; j < MAX_CITIES; j++) {
if (dist[city][j] < min && !visited[j]) {
min = dist[city][j];
}
}
lb += min;
}
}
return lb;
}
// Function to find the minimum cost tour using Branch and Bound
void tsp(int city, int level, int cost) {
if (level == MAX_CITIES) {
if (cost + dist[city][0] < min_cost) {
min_cost = cost + dist[city][0]; // Calculate total cost including return to starting city
}
return;
}
for (int i = 0; i < MAX_CITIES; i++) {
if (!visited[i]) {
visited[i] = 1;
tsp(i, level + 1, cost + dist[city][i]);
visited[i] = 0; // Backtrack
}
}
}
int main() {
int n;
// Get the number of cities
printf("Enter the number of cities: ");
scanf("%d", &n);
// Get the distance matrix
printf("Enter the distance matrix:\n");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &dist[i][j]);
}
}
// Initialize visited array
for (int i = 0; i < n; i++) {
visited[i] = 0;
}
visited[0] = 1; // Start from city 0
tsp(0, 1, 0);
printf("Minimum cost of the tour: %d\n", min_cost);
return 0;
}Explanation:
- Initialization:
dist[MAX_CITIES][MAX_CITIES]: A 2D array to store the distances between cities.visited[MAX_CITIES]: An array to keep track of visited cities.min_cost: A variable to store the minimum cost of the tour, initialized to infinity (INT_MAX).
lower_bound()function:- Calculates a lower bound on the cost of the remaining tour from a given city.
- For each unvisited city, finds the minimum distance to any other unvisited city.
- Sums these minimum distances to get a lower bound on the remaining cost.
tsp()function:- Implements the recursive Branch and Bound algorithm.
city: The current city being visited.level: The current level in the search tree.cost: The cost of the path traversed so far.- If all cities have been visited (
level == MAX_CITIES):- Calculate the total cost by adding the distance from the current city back to the starting city.
- Update
min_costif the total cost is less than the current minimum.
- Otherwise:
- Iterate through all unvisited cities:
- Mark the city as visited.
- Recursively call
tsp()with the next city, increased level, and updated cost. - Unmark the city (backtrack).
- Iterate through all unvisited cities:
main()function:- Reads the number of cities and the distance matrix from the user.
- Initializes the
visitedarray. - Calls the
tsp()function to find the minimum cost tour, starting from city 0. - Prints the minimum cost of the tour.
Output:
Enter the number of cities: 4
Enter the distance matrix:
0 10 15 20
10 0 35 25
15 35 0 30
20 25 30 0
Minimum cost of the tour: 80 //C++ CODE FOR TSP
#include <iostream>
#include <vector>
#include <limits.h>
using namespace std;
const int MAX_CITIES = 20;
class TSP {
private:
vector<vector<int>> dist; // Matrix to store distances between cities
vector<bool> visited; // Array to keep track of visited cities
int n; // Number of cities
int min_cost; // Minimum cost of the tour
// Function to calculate the lower bound for a given path
int lower_bound(int city) {
int lb = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
int min = INT_MAX;
for (int j = 0; j < n; j++) {
if (dist[city][j] < min && !visited[j]) {
min = dist[city][j];
}
}
lb += min;
}
}
return lb;
}
// Function to find the minimum cost tour using Branch and Bound
void tsp(int city, int level, int cost) {
if (level == n) {
if (cost + dist[city][0] < min_cost) {
min_cost = cost + dist[city][0]; // Calculate total cost including return to starting city
}
return;
}
for (int i = 0; i < n; i++) {
if (!visited[i]) {
visited[i] = true;
tsp(i, level + 1, cost + dist[city][i]);
visited[i] = false; // Backtrack
}
}
}
public:
TSP(int numCities) : n(numCities), dist(n, vector<int>(n)), visited(n, false), min_cost(INT_MAX) {}
void setDistances(const vector<vector<int>>& distances) {
dist = distances;
}
void findMinCostTour() {
visited[0] = true; // Start from city 0
tsp(0, 1, 0);
}
int getMinCost() const {
return min_cost;
}
};
int main() {
int n;
cout << "Enter the number of cities: ";
cin >> n;
vector<vector<int>> distances(n, vector<int>(n));
cout << "Enter the distance matrix:\n";
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> distances[i][j];
}
}
TSP tspSolver(n);
tspSolver.setDistances(distances);
tspSolver.findMinCostTour();
cout << "Minimum cost of the tour: " << tspSolver.getMinCost() << endl;
return 0;
}
// C code for NQueen
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// Function to print the chessboard with queens placed
void printSolution(int board[], int N) {
// Print the chessboard row by row
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
// If the queen is placed in this column, print 'Q'
if (board[i] == j)
printf("Q ");
else
printf(". "); // Otherwise, print an empty space
}
printf("\n");
}
printf("\n");
}
// Function to check if a queen can be safely placed at position (row, col)
bool isSafe(int board[], int row, int col) {
for (int i = 0; i < row; i++) {
// Check if there is a queen already in the same column
// or if the current position (row, col) is attacked diagonally
if (board[i] == col ||
board[i] - i == col - row || // Check for left diagonal conflict
board[i] + i == col + row) { // Check for right diagonal conflict
return false; // If any conflict, return false
}
}
return true; // No conflicts, safe to place queen
}
// Backtracking function to solve the N-Queen problem
bool solveNQueen(int board[], int row, int N) {
// If all queens are placed, we have found a solution
if (row == N) {
printSolution(board, N); // Print the solution
return true; // Return true to indicate a solution is found
}
bool res = false; // Variable to store if any solution is found
// Try placing a queen in all columns of the current row
for (int col = 0; col < N; col++) {
// Check if it's safe to place the queen in column `col` of row `row`
if (isSafe(board, row, col)) {
board[row] = col; // Place the queen in the current position
// Recursively try to place queens in the next row
res = solveNQueen(board, row + 1, N) || res;
board[row] = -1; // Backtrack, remove the queen and try next column
}
}
return res; // Return true if a solution is found, false otherwise
}
// Function to start the Branch and Bound method to solve the N-Queen problem
void branchAndBoundNQueen(int N) {
// Dynamically allocate memory for the board (1D array to store column indices of queens)
int* board = (int*)malloc(N * sizeof(int));
// Initialize the board with no queens placed (-1 indicates unassigned column)
for (int i = 0; i < N; i++) {
board[i] = -1; // All rows are initially empty
}
// Call the recursive backtracking function starting from the first row
if (!solveNQueen(board, 0, N)) {
// If no solution is found, print a message
printf("No solution exists\n");
}
// Free dynamically allocated memory to avoid memory leaks
free(board);
}
int main() {
int N;
// Prompt user to input the value of N for the N-Queen problem
printf("Enter the value of N for the N-Queen problem: ");
scanf("%d", &N);
// Ensure that N is greater than or equal to 4, as the problem has no solution for N < 4
if (N < 4) {
printf("No solution exists for N < 4\n");
return 0; // Exit the program early as there is no solution for N < 4
}
// Start the Branch and Bound process to solve the N-Queen problem
branchAndBoundNQueen(N);
return 0;
}
Branch and Bound method for NQUEEN, KNAPSACK and Job Assignment problems
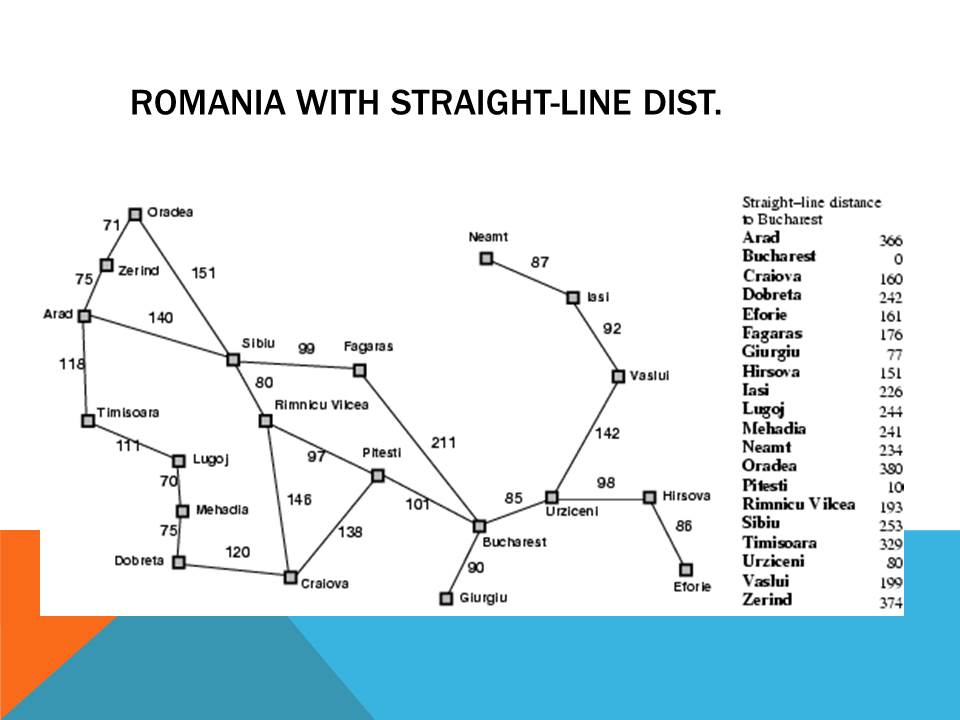
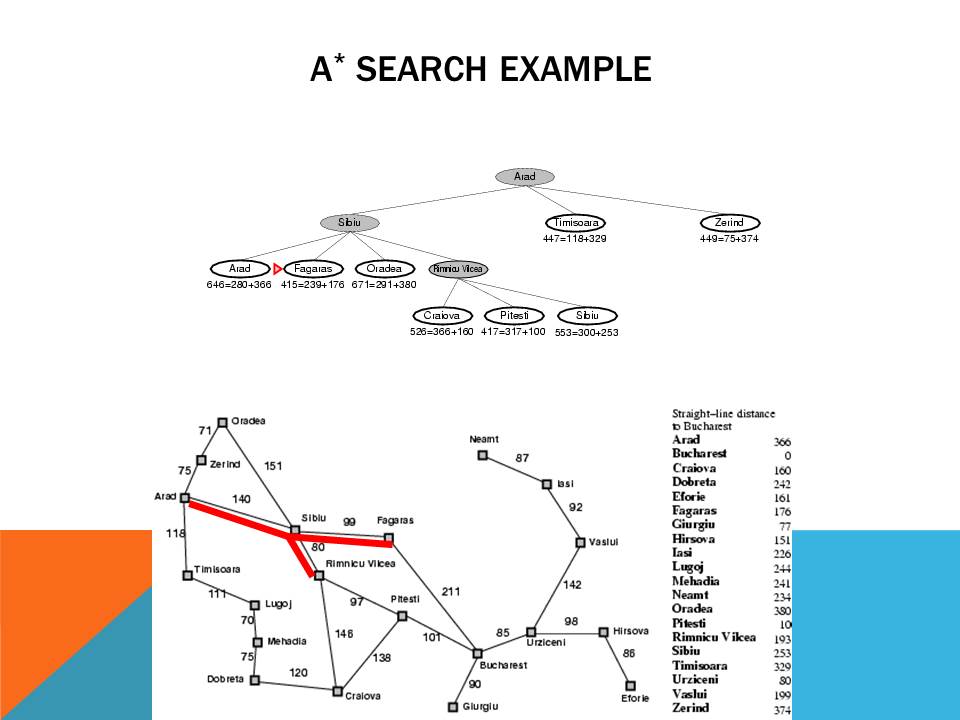
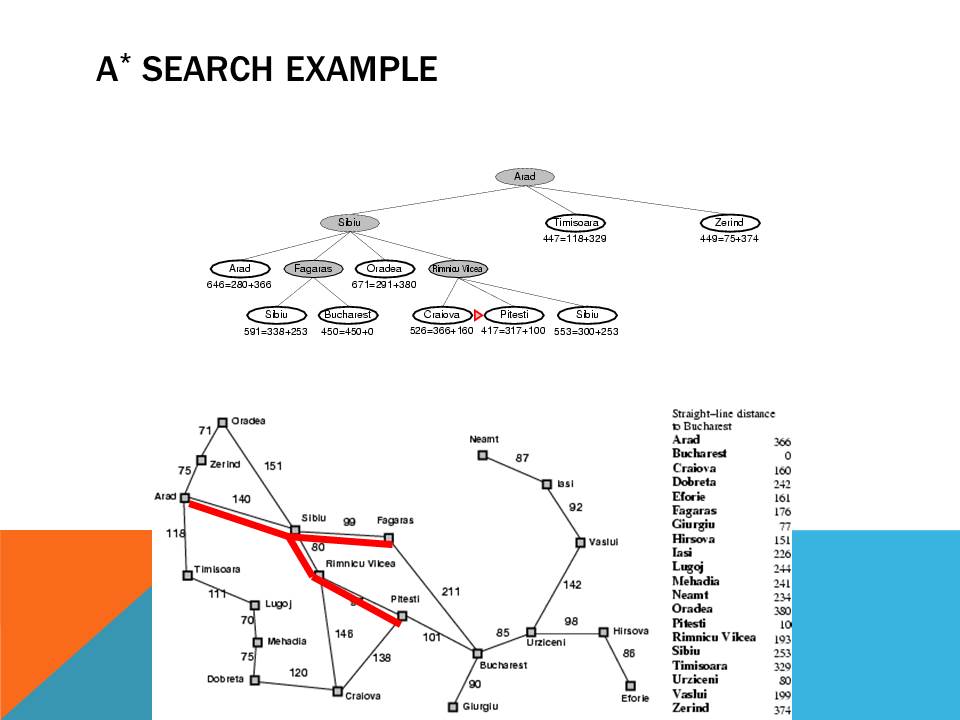
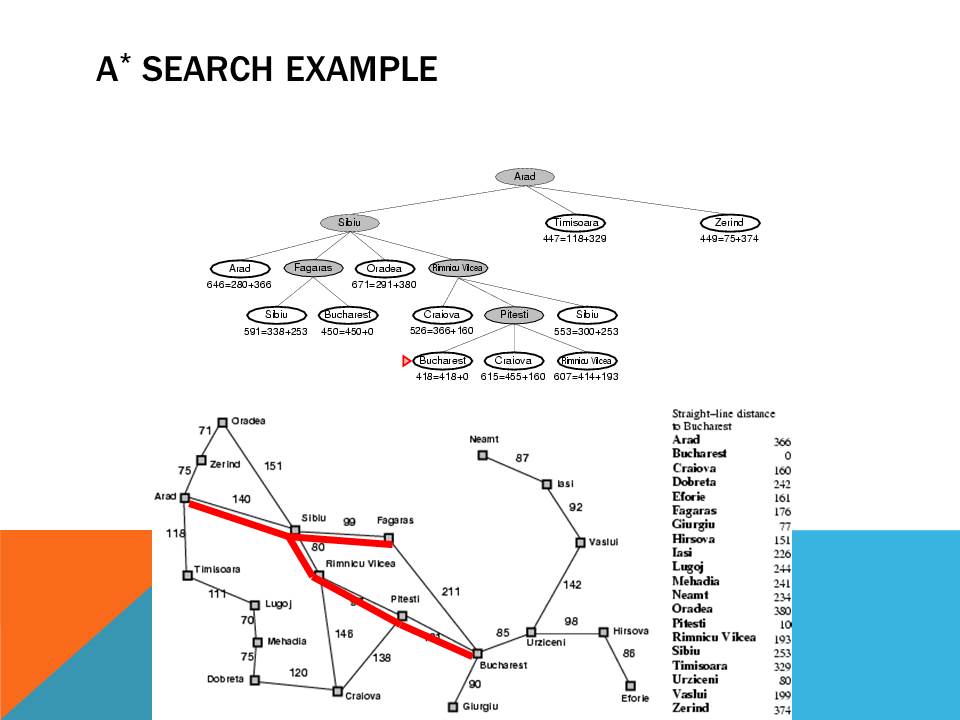
A* algorithm is a LC-BB