- Topdown (memoization) vs bottom-up (tabulation)
- Solving LCS (Longest Common Sub-Sequence) using dynamic programming
- Solving Fibonacci sequence problem using dynamic programming
- Solving matrix chain multiplication problems using dynamic programming
- Solving 0-1 knapsack using dynamic programming
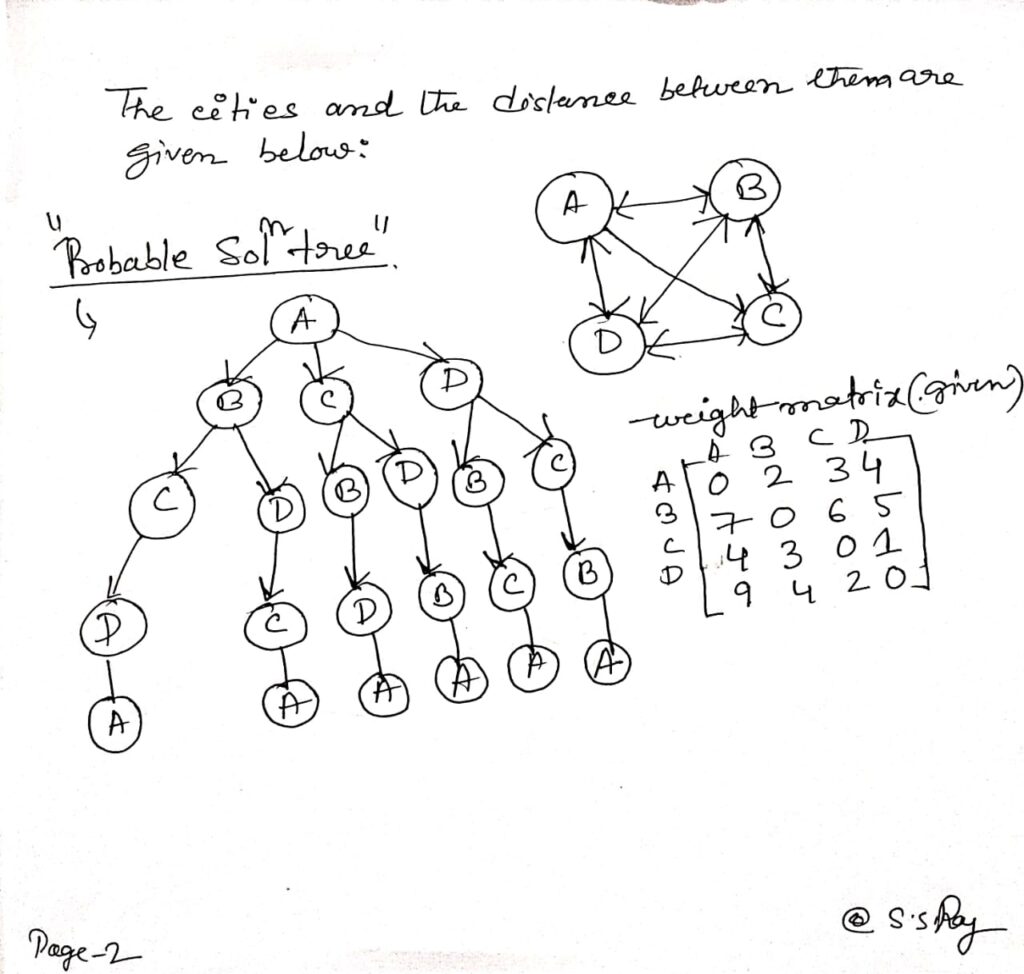
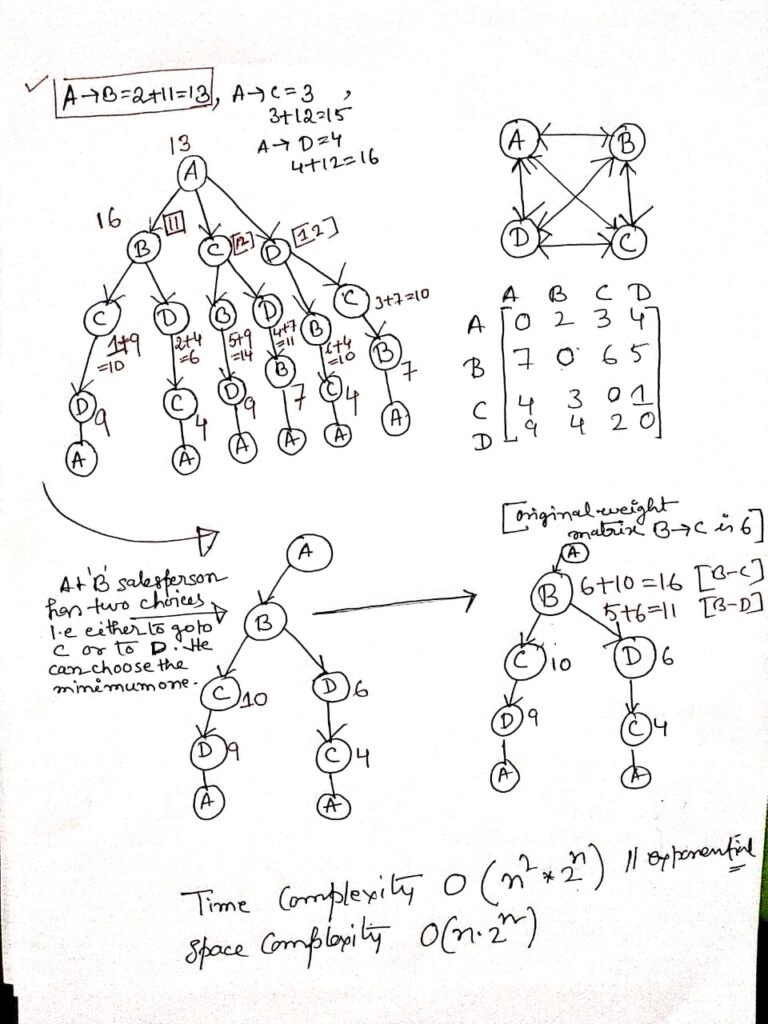
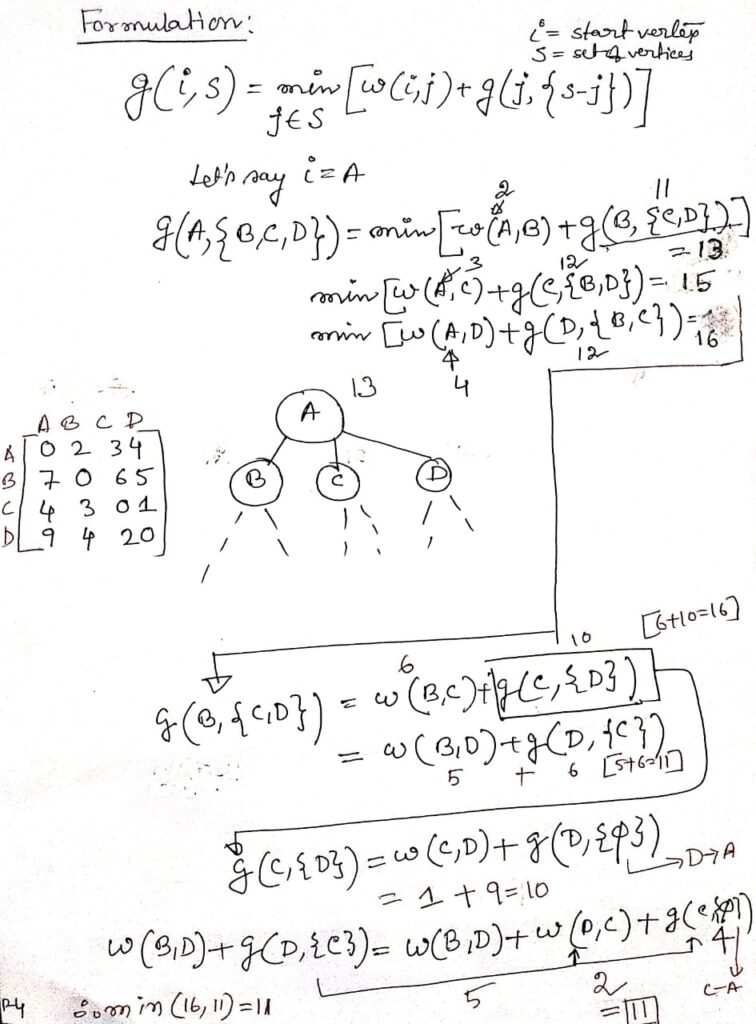
- Solving TSP(Travelling Salesperson Problem) using dynamic programming
- Solving Climbing stairs using dynamic programming
The bottom-up approach [tabulation method] in dynamic programming starts by solving the smallest subproblems first, then uses these solutions to build up to larger subproblems until the entire problem is solved. This approach works by filling out a table (usually iteratively) that stores the solutions to all subproblems, ensuring that each one is solved only once.
In contrast, the top-down approach solves the problem in a more natural, recursive manner. During recursion, it checks whether a subproblem has already been solved (often using a technique called Memoization) to avoid redundant calculations. If a solution has already been computed, it uses the stored result; if not, it solves the subproblem and stores the result for future use.
There has been some confusion about the terminology used to describe these approaches. Some earlier descriptions inaccurately stated that “bottom-up is memoization,” but this is misleading. Infact, memoization is typically associated with the top-down approach, where subproblems are solved recursively and results are cached. Bottom-up involves iterating over subproblems, gradually solving them from the smallest to the largest.
While memoization is a common technique used in top-down dynamic programming, it is not a separate form of dynamic programming; rather, it is a specific strategy for implementing top-down solutions. As a result, it’s important to use precise language when discussing these concepts to avoid confusion. For clarity, it’s best to rely on well-established academic sources to define these approaches and avoid ambiguous or inaccurate terminology.
Memoization is a technique used in dynamic programming to optimize recursive algorithms by storing the results of expensive function calls and reusing them when the same inputs occur again. This approach is typically applied in top-down dynamic programming.
In a memoized solution, when a function is called with a specific set of parameters, the algorithm first checks if the result for those parameters has already been computed and stored. If so, it retrieves the cached result, avoiding the need to recompute it. If the result has not been computed, the function executes its logic, calculates the result, and stores it for future use. This process significantly reduces redundant calculations, especially in problems with overlapping subproblems. For example, in the Fibonacci sequence calculation, without memoization, the function may recalculate the same Fibonacci numbers multiple times. With memoization, each Fibonacci number is computed only once, and subsequent requests for the same value are served from the cache. Memoization is often implemented using a hash table or a 2D array to store the results of subproblems. It helps convert a potentially exponential-time recursive algorithm into a more efficient one, often reducing the time complexity to polynomial time. While memoization is effective in problems with overlapping subproblems, it requires additional space for the cache, which may be a concern in memory-limited environments.
Solving LCS (Longest Common Sub sequence) using dynamic programming
#include <stdio.h>
#include <string.h>
int i, j, m, n, dp[20][20]; // Dynamic programming table
char seq1[20], seq2[20], direction[20][20]; // Sequences and direction table
void printLCS(int i, int j) {
if (i == 0 || j == 0)
return;
if (direction[i][j] == 'c') {
printLCS(i - 1, j - 1);
printf("%c", seq1[i - 1]);
} else if (direction[i][j] == 'u')
printLCS(i - 1, j);
else
printLCS(i, j - 1);
}
void longestCommonSubsequence() {
for (i = 0; i <= m; i++)
dp[i][0] = 0;
for (i = 0; i <= n; i++)
dp[0][i] = 0;
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++) {
if (seq1[i - 1] == seq2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
direction[i][j] = 'c';
} else if (dp[i - 1][j] >= dp[i][j - 1]) {
dp[i][j] = dp[i - 1][j];
direction[i][j] = 'u';
} else {
dp[i][j] = dp[i][j - 1];
direction[i][j] = 'l';
}
}
}
int main() {
printf("Enter the length of the 1st sequence: ");
scanf("%d", &m);
printf("Enter the 1st sequence: ");
scanf("%s", seq1);
printf("Enter the length of the 2nd sequence: ");
scanf("%d", &n);
printf("Enter the 2nd sequence: ");
scanf("%s", seq2);
printf("\nThe Longest Common Subsequence is ");
longestCommonSubsequence();
printLCS(m, n);
return 0;
}
Output :
Enter the length of the 1st sequence: 5
Enter the 1st sequence: ABCDE
Enter the length of the 2nd sequence: 4
Enter the 2nd sequence: SCDEF
The Longest Common Subsequence is CDE
Process returned 0 (0x0) execution time : 12.934 s
Press any key to continue.
Example 2.
#include <stdio.h>
#include <string.h>
#define MAX 1001
char string1[MAX], string2[MAX];
int lcsTable[MAX][MAX];
char currentSeq[MAX];
int lcsLength;
char uniqueResults[MAX][MAX];
int resultCount = 0;
int checkExistence(char* str) {
for(int i = 0; i < resultCount; i++) {
if(strcmp(uniqueResults[i], str) == 0) {
return 1;
}
}
return 0;
}
void saveLCS(int position) {
if(position == 0) {
if(!checkExistence(currentSeq)) {
strcpy(uniqueResults[resultCount++], currentSeq);
}
}
}
void computeLCSMatrix(int m, int n) {
for(int i = 0; i <= m; i++) {
for(int j = 0; j <= n; j++) {
if(i == 0 || j == 0)
lcsTable[i][j] = 0;
else if(string1[i-1] == string2[j-1])
lcsTable[i][j] = lcsTable[i-1][j-1] + 1;
else
lcsTable[i][j] = (lcsTable[i-1][j] > lcsTable[i][j-1]) ? lcsTable[i-1][j] : lcsTable[i][j-1];
}
}
lcsLength = lcsTable[m][n];
}
void retrieveLCS(int i, int j, int position) {
if(position == 0) {
saveLCS(position);
return;
}
if(i == 0 || j == 0) {
return;
}
if(string1[i-1] == string2[j-1]) {
currentSeq[position-1] = string1[i-1];
retrieveLCS(i-1, j-1, position-1);
}
else {
if(lcsTable[i-1][j] == lcsTable[i][j-1]) {
retrieveLCS(i-1, j, position);
retrieveLCS(i, j-1, position);
}
else if(lcsTable[i-1][j] > lcsTable[i][j-1]) {
retrieveLCS(i-1, j, position);
}
else {
retrieveLCS(i, j-1, position);
}
}
}
int main() {
fgets(string1, MAX, stdin);
fgets(string2, MAX, stdin);
string1[strcspn(string1, "\n")] = 0;
string2[strcspn(string2, "\n")] = 0;
int len1 = strlen(string1);
int len2 = strlen(string2);
if(len1 == 0 || len2 == 0) {
printf("\n0\n");
return 0;
}
computeLCSMatrix(len1, len2);
memset(currentSeq, 0, MAX);
resultCount = 0;
retrieveLCS(len1, len2, lcsLength);
for(int i = 0; i < resultCount; i++) {
printf("%s\n", uniqueResults[i]);
}
printf("The length of the Longest Common Subsequence is: %d", lcsLength);
return 0;
}
Fibonacci Sequence
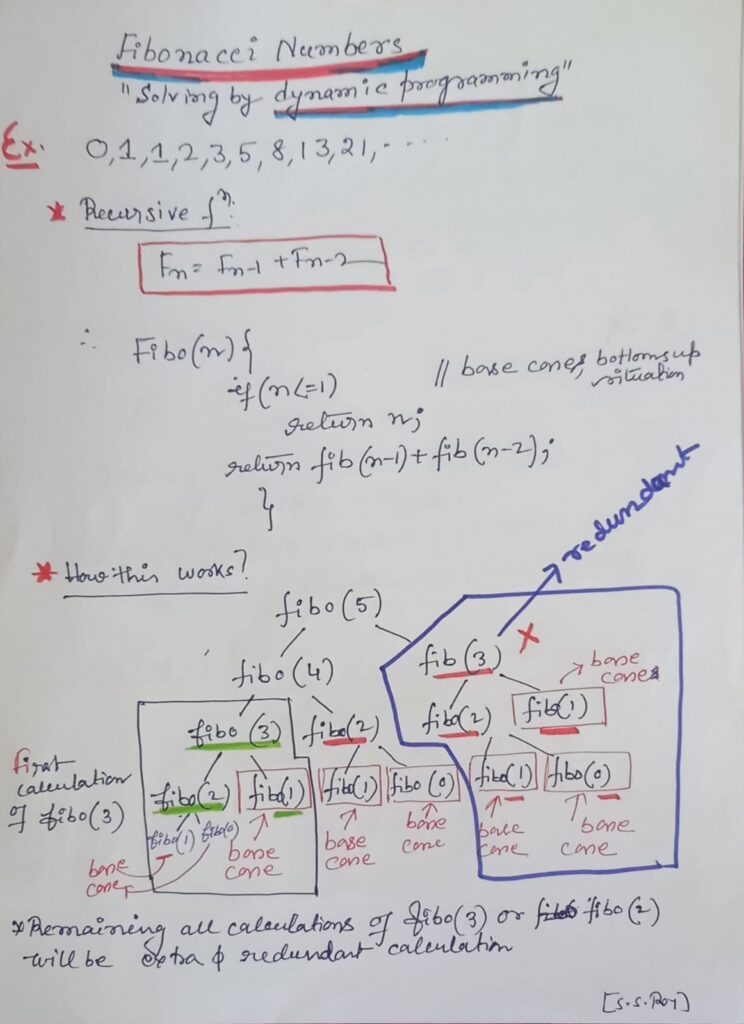


//C++ Top Down(Memoization)for fibonacci
#include <iostream>
#include <vector>
using namespace std;
class Fibonacci {
public:
Fibonacci(int n) : memo_(n + 1, -1) {}
int calculate(int n) {
if (n <= 1) {
return n;
}
if (memo_[n] != -1) {
return memo_[n];
}
memo_[n] = calculate(n - 1) + calculate(n - 2);
return memo_[n];
}
private:
vector<int> memo_;
};
int main() {
int n;
cout << "Enter the value of n: ";
cin >> n;
Fibonacci fib(n);
int result = fib.calculate(n);
cout << "Fibonacci(" << n << ") = " << result << endl;
cout << "Fibonacci Series: ";
for (int i = 0; i <= n; i++) {
cout << fib.calculate(i) << " ";
}
cout << endl;
return 0;
}
Output:
Enter the value of n: 10
Fibonacci(10) = 55
Fibonacci Series: 0 1 1 2 3 5 8 13 21 34 55 //C Top Down(Memoization)& for fibonacci
#include <stdio.h>
#include <limits.h>
// Function to calculate Fibonacci number using top-down dynamic programming (memoization)
int fib(int n, int *memo) {
// Base cases: If n is 0 or 1, return n directly (Fibonacci of 0 is 0, Fibonacci of 1 is 1)
if (n <= 1) {
return n;
}
// If the result is already computed, return it directly from the memoization array
if (memo[n] != -1) {
return memo[n];
}
// Calculate the Fibonacci number recursively using the definition: fib(n) = fib(n-1) + fib(n-2)
memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
// Store the calculated result in the memoization array for future use
return memo[n];
}
int main() {
int n;
printf("Enter the value of n: "); // Prompt the user to enter the value of n
scanf("%d", &n); // Read the input value from the user and store it in n
// Initialize memoization array with -1 (indicating uncomputed values)
int memo[n + 1];
for (int i = 0; i <= n; i++) {
memo[i] = -1;
}
int result = fib(n, memo); // Call the fib function to calculate the nth Fibonacci number
printf("Fibonacci(%d) = %d\n", n, result); // Print the calculated Fibonacci number
// Print the Fibonacci series
printf("Fibonacci Series: ");
for (int i = 0; i <= n; i++) {
printf("%d ", fib(i, memo));
}
printf("\n");
return 0; // Indicate successful program execution
}
Output :
Enter the value of n: 6
Fibonacci(6) = 8
Fibonacci Series: 0 1 1 2 3 5 8
Process returned 0 (0x0) execution time : 2.727 s
Press any key to continue.
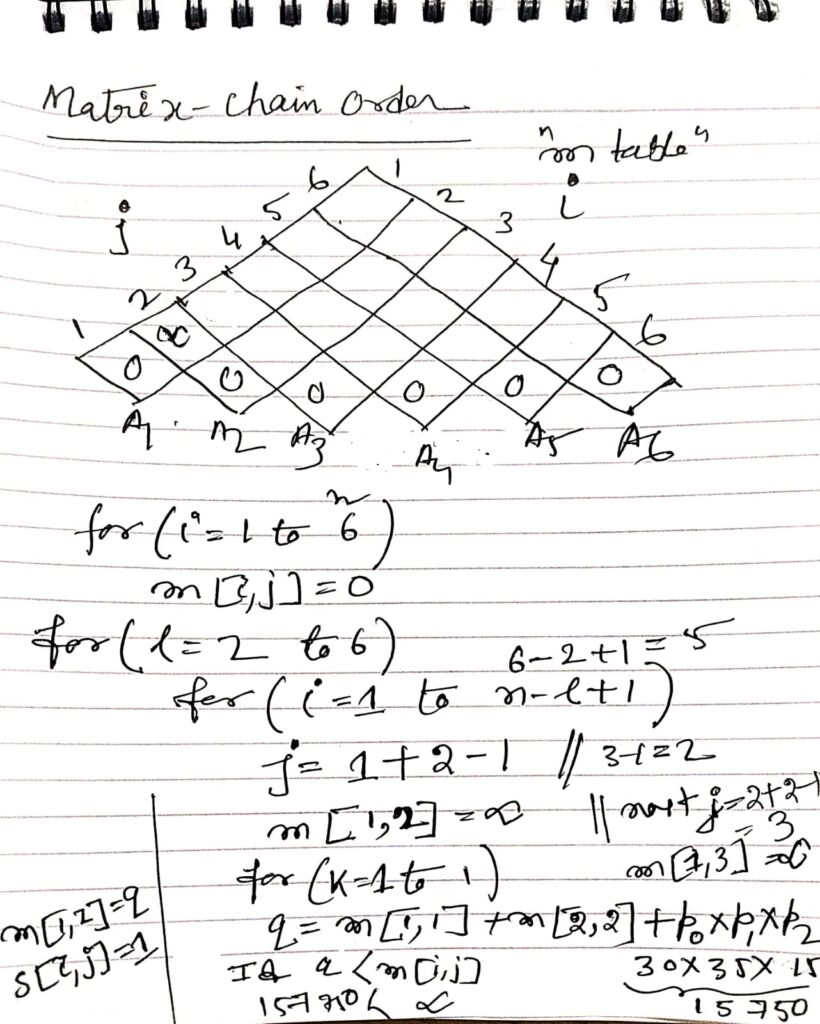
Matrix Chain Multiplication using Dynamic Programming

/*
The given code follows a Bottom-up[TABULATION METHOD] approach of dynamic programming for solving the Matrix Chain Multiplication problem. This approach builds the solution incrementally by solving smaller subproblems first and combining their results to solve larger subproblems.*/
#include <stdio.h> // Include the standard input/output library for functions like printf and scanf
#include <limits.h> // Include the limits.h library for using INT_MAX for initialization
// Function to compute the minimum number of scalar multiplications
// and store the optimal split points
int MatrixChainOrder(int p[], int i, int j, int s[10][10]) {
if (i == j) {
// Base case: If there's only one matrix, no multiplication is needed
return 0;
}
int k;
int min = INT_MAX; // Initialize 'min' with the maximum possible value
// to ensure it gets updated with the actual minimum cost
int count;
// Try all possible split points 'k' for the given subproblem (from i to j)
for (k = i; k < j; k++) {
// Calculate the cost of multiplying the subproblems recursively
count = MatrixChainOrder(p, i, k, s) +
MatrixChainOrder(p, k + 1, j, s) +
p[i - 1] * p[k] * p[j]; // Cost of multiplying matrices at split point 'k'
// Update the minimum cost and store the optimal split point
if (count < min) {
min = count;
s[i][j] = k; // Store the optimal split point 'k' in the 's' array
}
}
return min; // Return the minimum cost of multiplying the subproblem
}
// Function to print the optimal parenthesization of matrix multiplications
void printParenthesis(int i, int j, int s[10][10]) {
if (i == j) {
// Base case: If there's only one matrix, print "A<i>"
printf("A%d", i);
} else {
printf("("); // Print opening parenthesis
printParenthesis(i, s[i][j], s); // Recursively print the left subproblem
printParenthesis(s[i][j] + 1, j, s); // Recursively print the right subproblem
printf(")"); // Print closing parenthesis
}
}
// Driver code
int main() {
int n;
printf("Enter the number of matrices: ");
scanf("%d", &n); // Read the number of matrices from the user
int arr[n + 1];
int s[10][10]; // 2D array to store the optimal split points
printf("Enter the dimensions of the matrices: \n");
for (int i = 0; i <= n; i++) {
printf("Dimension %d: ", i);
scanf("%d", &arr[i]); // Read the dimensions of each matrix from the user
}
int minMultiplications = MatrixChainOrder(arr, 1, n, s); // Calculate the minimum number of multiplications
printf("Minimum number of multiplications is: %d\n", minMultiplications);
printf("Optimal Parenthesization: ");
printParenthesis(1, n, s); // Print the optimal parenthesization
printf("\n");
return 0; // Indicate successful program execution
}
Output :
Enter the number of matrices: 6
Enter the dimensions of the matrices:
Dimension 0: 30
Dimension 1: 35
Dimension 2: 15
Dimension 3: 5
Dimension 4: 10
Dimension 5: 20
Dimension 6: 25
Minimum number of multiplications is: 15125
Optimal Parenthesization: ((A1(A2A3))((A4A5)A6))
Process returned 0 (0x0) execution time : 55.221 s
Press any key to continue.
The above-given code demonstrates a top-down approach to solving the Matrix Chain Multiplication problem.Here’s why:
- Recursive Structure: The
MatrixChainOrderfunction is recursive. It breaks down the problem into smaller subproblems (finding the optimal multiplication order for smaller subchains of matrices) and then recursively solves those subproblems. - Memoization: The code uses a 2D array
sto store the results of already computed subproblems. This memoization technique prevents redundant calculations, significantly improving the efficiency of the algorithm.
Key Characteristics of Top-Down Approach:
- Divide and Conquer: The problem is divided into smaller subproblems.
- Recursion: Smaller subproblems are solved recursively.
- Memoization: Results of subproblems are stored to avoid redundant calculations.
In contrast, a bottom-up approach (dynamic programming) would:
- Iteratively solve the problem: Start with the smallest subproblems and gradually build up solutions for larger subproblems.
- Tabulation: Store the results of subproblems in a table and use them to calculate solutions for larger subproblems.
While both approaches can solve the Matrix Chain Multiplication problem, the top-down approach with memoization (as shown in the code) often provides a more intuitive and elegant implementation.
//C++ code for Matrix Chain Order
#include <iostream>
#include <vector>
#include <limits>
using namespace std;
// Function to compute the minimum number of scalar multiplications
// and store the optimal split points
int MatrixChainOrder(const vector<int>& p, int i, int j, vector<vector<int>>& s) {
if (i == j) {
return 0;
}
int min = numeric_limits<int>::max();
int count;
for (int k = i; k < j; k++) {
count = MatrixChainOrder(p, i, k, s) +
MatrixChainOrder(p, k + 1, j, s) +
p[i - 1] * p[k] * p[j];
if (count < min) {
min = count;
s[i][j] = k;
}
}
return min;
}
// Function to print the optimal parenthesization of matrix multiplications
void printParenthesis(int i, int j, const vector<vector<int>>& s) {
if (i == j) {
cout << "A" << i;
} else {
cout << "(";
printParenthesis(i, s[i][j], s);
printParenthesis(s[i][j] + 1, j, s);
cout << ")";
}
}
int main() {
int n;
cout << "Enter the number of matrices: ";
cin >> n;
vector<int> arr(n + 1);
vector<vector<int>> s(n + 1, vector<int>(n + 1, 0));
cout << "Enter the dimensions of the matrices: \n";
for (int i = 0; i <= n; i++) {
cout << "Dimension " << i << ": ";
cin >> arr[i];
}
int minMultiplications = MatrixChainOrder(arr, 1, n, s);
cout << "Minimum number of multiplications is: " << minMultiplications << endl;
cout << "Optimal Parenthesization: ";
printParenthesis(1, n, s);
cout << endl;
return 0;
}
Output :
Enter the value of n: 10
Fibonacci(10) = 55
Fibonacci Series: 0 1 1 2 3 5 8 13 21 34 55 Solving 0-1 knapsack using dynamic programming
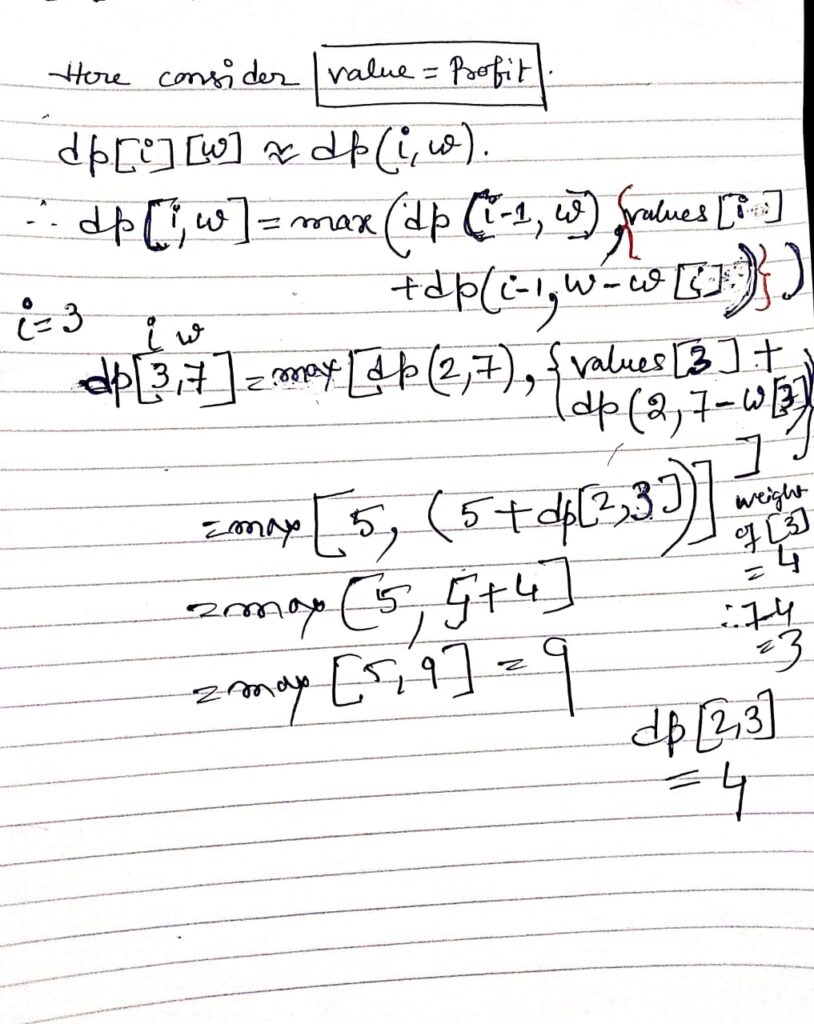
// Algorithm Function knapsack(values[], weights[], n, capacity):
Create a 2D array dp[n+1][capacity+1]
For i = 0 to n:
For w = 0 to capacity:
If i == 0 or w == 0:
dp[i][w] = 0
Else If weights[i-1] <= w:
dp[i][w] = max(dp[i-1][w], values[i-1] + dp[i-1][w-weights[i-1]])
Else:
dp[i][w] = dp[i-1][w]
w = capacity
Print "Items included: "
For i = n to 1:
If dp[i][w] != dp[i-1][w]:
Print i
w = w - weights[i-1]
Return dp[n][capacity]
Function max(a, b):
If a > b:
Return a
Else:
Return b
Main:
values = [1, 4, 5, 7]
weights = [1, 3, 4, 5]
capacity = 7
n = Length of values
max_value = knapsack(values, weights, n, capacity)
//C Code for 0-1 knapsack
#include <stdio.h>
// Function to find the maximum of two integers
int max(int a, int b) {
return (a > b) ? a : b;
}
// Function to implement the 0/1 Knapsack problem using dynamic programming
int knapsack(int values[], int weights[], int n, int capacity) {
int dp[n + 1][capacity + 1];
// Initialize the dp table
for (int i = 0; i <= n; i++) {
for (int w = 0; w <= capacity; w++) {
if (i == 0 || w == 0) {
dp[i][w] = 0;
} else if (weights[i - 1] <= w) {
dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]]);
} else {
dp[i][w] = dp[i - 1][w];
}
}
}
// Print the items included in the knapsack
printf("Items included: ");
int w = capacity;
for (int i = n; i > 0; i--) {
if (dp[i][w] != dp[i - 1][w]) {
printf("%d ", i);
w = w - weights[i - 1];
}
}
printf("\n");
return dp[n][capacity];
}
int main() {
int values[] = {1, 4, 5, 7};
int weights[] = {1, 3, 4, 5};
int capacity = 7;
int n = sizeof(values) / sizeof(values[0]);
int max_value = knapsack(values, weights, n, capacity);
printf("Maximum value that can be obtained: %d\n", max_value);
return 0;
}
Output:
Items included: 4 3 1
Maximum value that can be obtained: 17
//Explanations
In the equation:
dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])```
- First argument: dp[i - 1][w]
This represents the maximum value obtainable with the first `i - 1` items and a knapsack capacity of `w`. It corresponds to the scenario where we **exclude** the current `i`th item from the knapsack.
- Second argument: `values[i - 1] + dp[i - 1][w - weights[i - 1]]`
This represents the maximum value obtainable by **including** the `i`-th item in the knapsack. It is the value of the `i`-th item (`values[i - 1]`) plus the maximum value that can be achieved with the remaining capacity (`w - weights[i - 1]`) and the first `i - 1` items.//C++ code for 0-1 knapsack
#include <iostream>
#include <vector>
using namespace std;
class Knapsack {
public:
Knapsack(const vector<int>& values, const vector<int>& weights, int capacity)
: values_(values), weights_(weights), capacity_(capacity),
n_(values.size()), dp_(n_ + 1, vector<int>(capacity_ + 1, 0)) {}
int solve() {
for (int i = 1; i <= n_; ++i) {
for (int w = 1; w <= capacity_; ++w) {
if (weights_[i - 1] <= w) {
dp_[i][w] = max(dp_[i - 1][w], values_[i - 1] + dp_[i - 1][w - weights_[i - 1]]);
} else {
dp_[i][w] = dp_[i - 1][w];
}
}
}
return dp_[n_][capacity_];
}
void printIncludedItems() const {
cout << "Items included: ";
int w = capacity_;
for (int i = n_; i > 0; --i) {
if (dp_[i][w] != dp_[i - 1][w]) {
cout << i << " ";
w -= weights_[i - 1];
}
}
cout << endl;
}
private:
vector<int> values_;
vector<int> weights_;
int capacity_;
int n_;
vector<vector<int>> dp_;
};
int main() {
vector<int> values = {1, 4, 5, 7};
vector<int> weights = {1, 3, 4, 5};
int capacity = 7;
Knapsack knapsack(values, weights, capacity);
int max_value = knapsack.solve();
cout << "Maximum value that can be obtained: " << max_value << endl;
knapsack.printIncludedItems();
return 0;
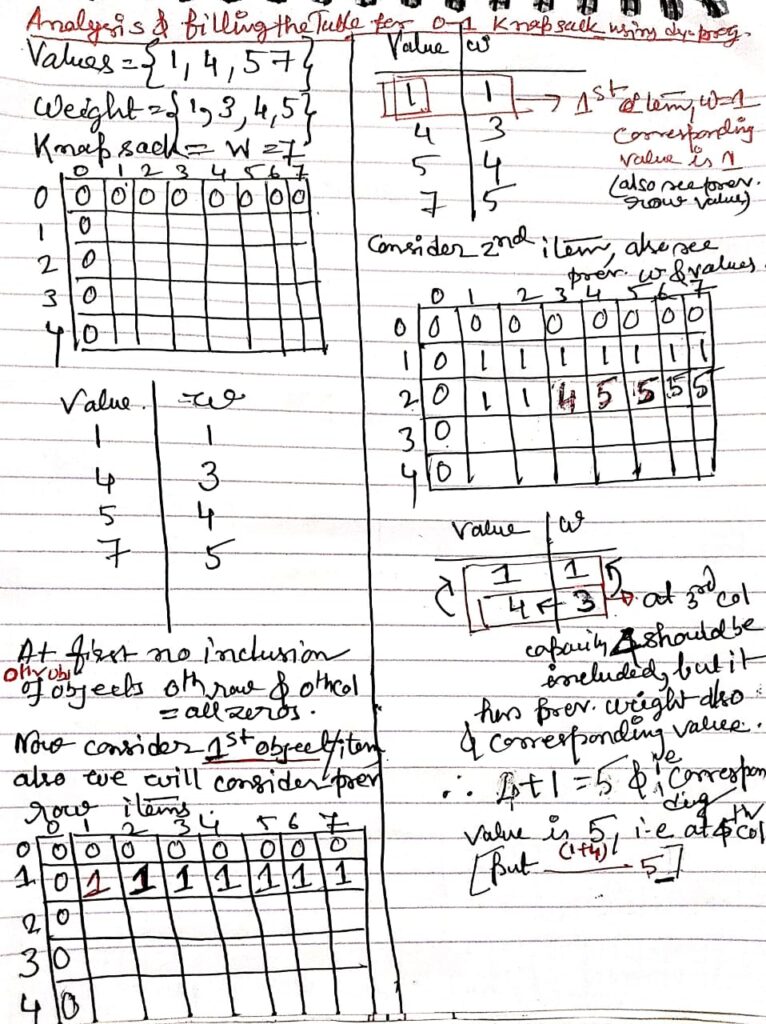
}Let’s solve the 0-1 Knapsack Problem step by step using a tabular form for the following example:
Example Input:
- Values: [1, 4, 5, 7]
- Weights: [1, 3, 4, 5]
- Knapsack Capacity: W=7W = 7
- Number of Items: n=4n = 4
We aim to fill a DP table, where dp[i][j]dp[i][j] represents the maximum value obtainable using the first ii items and knapsack capacity jj.
Step-by-Step Construction:
Initialization:
- Create a table with dimensions (n+1)×(W+1)
- Set all values in the first row (dp[0][j]) and the first column (dp[i][0]) to 0, as no value can be obtained with 0 items or capacity.
Step 1: Process Item 1 (Weight = 1, Value = 1):
- Iterate through capacities j=1j = 1 to W=7.
- For each j:
- If j≥1 (item’s weight), include the item.
- Otherwise, exclude it.
| dp[i][j] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Explanation:
- For j=1: Include item 1 → dp[1][1]=1= 1.
- For j>1: Since item 1’s weight is less than or equal to j, its value 1 is included.
Step 2: Process Item 2 (Weight = 3, Value = 4):
- Iterate through capacities j=1to W=7.
- For each j:
- If j≥3, decide to include or exclude item 2 based on which gives a higher value.
| dp[i][j] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| i=0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i=1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| i=2 | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
Explanation:
- For j=1,2: Exclude item 2 → dp[2][j]=dp[1][j]= 1.
- For j=3: Include item 2 → dp[2][3]=max(dp[1][3],4+dp[1][0])=4
- For j=4: Include item 2 → dp[2][4]=max(dp[1][4],4+dp[1][1])=5
- For j=5,6,7: Include item 2 → dp[2][j]= 5.
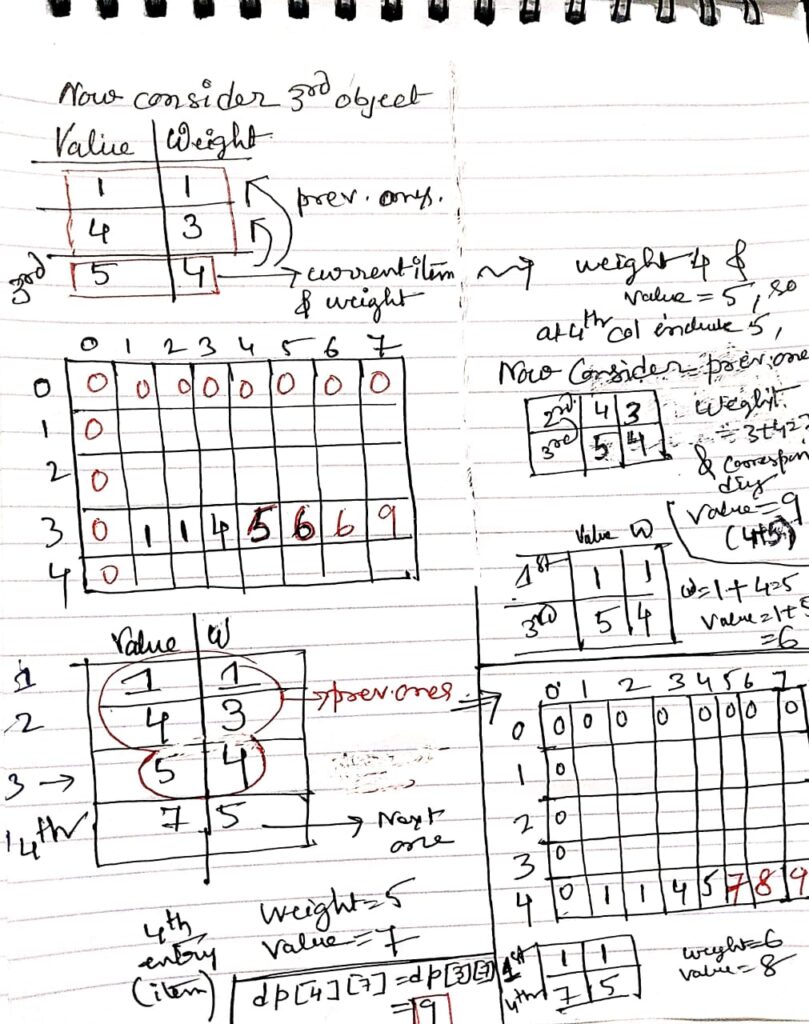
Step 3: Process Item 3 (Weight = 4, Value = 5):
- Iterate through capacities j=1 to W=7.
- For each j:
- If j≥4, decide to include or exclude item 3.
| dp[i][j] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| i = 2 | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| i = 3 | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
Explanation:
- For j=1,2,3: Exclude item 3 → dp[3][j]=dp[2][j].
- For j=4: Include item 3 → dp[3][4]=max(dp[2][4],5+dp[2][0])=5
- For j=5: Include item 3 → dp[3][5]=max(dp[2][5],5+dp[2][1])=6
- For j=6: Include item 3 → dp[3][6]=6
- For j=7: Include item 3 → dp[3][7]=9
Step 4: Process Item 4 (Weight = 5, Value = 7):
- Iterate through capacities j=1to W=7.
- For each j:
- If j≥5, decide to include or exclude item 4.
| dp[i][j] | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| i = 2 | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| i = 3 | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| i = 4 | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
Explanation:
- For j=1,2,3,4: Exclude item 4 → dp[4][j]=dp[3][j].
- For j=5: Include item 4 → dp[4][5]=max(dp[3][5],7+dp[3][0])=7
- For j=6: Include item 4 → dp[4][6]=8
- For j=7: Exclude item 4 → dp[4][7]=dp[3][7]=9
Final DP Table:
| Items \ Capacity | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| i = 2 | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
| i = 3 | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
| i = 4 | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
Final Solution:
- Maximum Value: 99
- Included Items: Item 2 and Item 3 (Weight = 3 and 4).
// C code for 0-1 knapsack using dynamic programming
#include <stdio.h>
#include <stdlib.h>
// Function to solve 0-1 Knapsack problem
int knapsack(int values[], int weights[], int n, int capacity) {
// Declare the DP table
int dp[n+1][capacity+1];
// Initialize the DP table
for (int i = 0; i <= n; i++) {
for (int w = 0; w <= capacity; w++) {
if (i == 0 || w == 0) {
dp[i][w] = 0; // Base case: No items or no capacity
} else if (weights[i-1] <= w) {
dp[i][w] = max(dp[i-1][w], values[i-1] + dp[i-1][w-weights[i-1]]);
} else {
dp[i][w] = dp[i-1][w]; // Exclude the current item
}
}
}
// Traceback to find included items (optional)
int w = capacity;
printf("Items included: ");
for (int i = n; i > 0 && w > 0; i--) {
if (dp[i][w] != dp[i-1][w]) {
printf("%d ", i); // Item i is included
w -= weights[i-1];
}
}
printf("\n");
// Return the maximum value
return dp[n][capacity];
}
// Utility function to get the maximum of two values
int max(int a, int b) {
return (a > b) ? a : b;
}
// Main function
int main() {
// Input example
int values[] = {1, 4, 5, 7};
int weights[] = {1, 3, 4, 5};
int capacity = 7;
int n = sizeof(values) / sizeof(values[0]);
// Solve knapsack problem
int max_value = knapsack(values, weights, n, capacity);
// Output result
printf("Maximum value in knapsack: %d\n", max_value);
return 0;
}
Does the recursive equation remain the same for the 0-1 knapsack problem, regardless of whether you use a greedy approach or dynamic programming.?
Yes, the recursive equation remains the same for the 0-1 knapsack problem, regardless of whether you use a greedy approach or dynamic programming.
Recursive Equation:
K(i, w) =
{
0 if i = 0 or w = 0
K(i-1, w) if wt[i-1] > w
max(val[i-1] + K(i-1, w-wt[i-1]), K(i-1, w)) otherwise
}
Explanation:
- This equation represents the core logic of the 0-1 Knapsack Problem.
- It defines how to calculate the maximum value that can be obtained by considering the first ‘i’ items with a knapsack capacity of ‘w’.
Key Points:
- Dynamic Programming: This approach utilizes the recursive equation to build a table of solutions to subproblems, avoiding redundant calculations.
- Greedy Approach: While the greedy approach doesn’t directly use the recursive equation in its implementation, the underlying decision-making process (e.g., selecting items based on value-to-weight ratio) still aims to maximize the overall value within the knapsack’s capacity.
In essence:
The recursive equation provides a fundamental framework for understanding the 0-1 Knapsack Problem. Both dynamic programming and greedy approaches strive to find the optimal solution, albeit with different strategies and computational complexities.
Solving TSP(Travelling Salesperson Problem) using dynamic programming