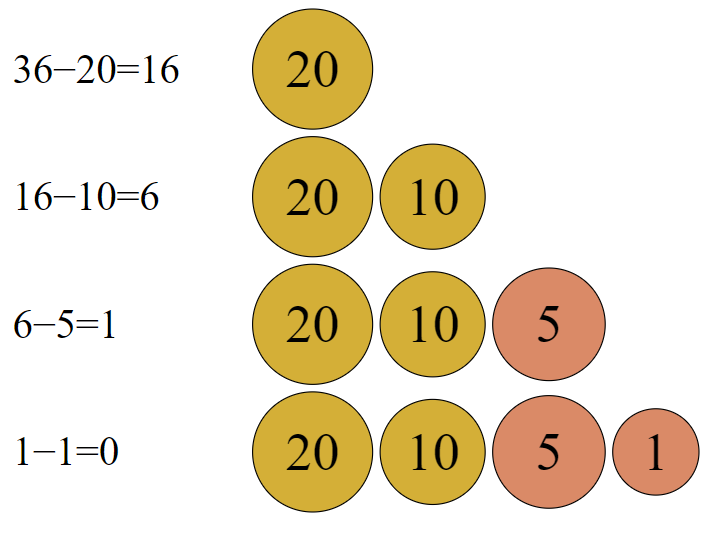
Minimum coin change problem : solving by greedy method

When it comes to finding the minimum number of coins to make change for a given amount, the Greedy Algorithm is particularly useful. This problem is often referred to as the “Minimum Coin Change Problem.” The goal is to determine the fewest number of coins needed to represent a given sum of money.

How Greedy Algorithm works for Minimum Coin Change?

The Greedy Algorithm works by selecting the largest denomination of coin that is less than or equal to the remaining amount, and repeats this process until the amount becomes zero. The idea is to always choose the coin with the highest value at each step, ensuring that the total number of coins used is minimized.

The minimum coin change algorithm

The Greedy Algorithm works by selecting the largest denomination of coin that is less than or equal to the remaining amount, and repeats this process until the amount becomes zero. The idea is to always choose the coin with the highest value at each step, ensuring that the total number of coins used is minimized.

  1. Sort the available coin denominations in descending order.
  2. Initialize a variable to keep track of the remaining amount to be represented.
  3. Iterate through the sorted denominations. At each step, choose the largest denomination that is less than or equal to the remaining amount.
  4. Subtract the chosen denomination from the remaining amount.
  5. Repeat steps 3-4 until the remaining amount becomes zero.
  6. The count of coins used represents the minimum number of coins required.

Let’s apply this algorithm to make change for $63 using coin denominations [25, 10, 5, 1].

  1. Sort Denominations: [25, 10, 5, 1]
  2. Initialize Variables:
    • remaining_amount = $63
    • coin_count = 0
  3. Greedy Coin Selection:
    • Iteration 1: Select 25, subtract from $63 (remaining_amount = $38), and increment coin_count (coin_count = 1).
    • Iteration 2: Select 25, subtract from $38 (remaining_amount = $13), and increment coin_count (coin_count = 2).
    • Iteration 3: Select 10, subtract from $13 (remaining_amount = $3), and increment coin_count (coin_count = 3).
    • Iteration 4: Select 1, subtract from $3 (remaining_amount = $2), and increment coin_count (coin_count = 4).
    • Iteration 5: Select 1, subtract from $2 (remaining_amount = $1), and increment coin_count (coin_count = 5).
    • Iteration 6: Select 1, subtract from $1 (remaining_amount = $0), and increment coin_count (coin_count = 6).
  4. Result: The minimum number of coins needed is 6.

This algorithmic approach provides a clear and engaging step-by-step process for finding the minimum number of coins to make change. It’s efficient and works well for certain scenarios, although it’s important to note its limitations in more complex cases where a dynamic programming approach might be necessary for optimality.

// This following method is an iterative method, keep an eye here further for  a recursive version of it.
#include<stdio.h>

void GreedyCoinCh(int coins[], int numCoins, int TrgtAmt) {
    // Sort the coins in descending order
    int i,j;
    for (i = 0; i < numCoins - 1; i++) {
        for (j = 0; j < numCoins - i - 1; j++) {
            if (coins[j] < coins[j + 1]) {
                // Swap if the current coin is smaller than the next one
                int temp = coins[j];
                coins[j] = coins[j + 1];
                coins[j + 1] = temp;
            }
        }
    }

    // Initialize variables
    int RestAmount = TrgtAmt;
    // Greedy approach: Select the largest coin at each step
    printf("Selected coins: ");
    for (i = 0; i < numCoins; i++) {
        while (RestAmount >= coins[i]) {
            // Use as many coins of the current denomination as possible
            printf("%d ", coins[i]);
            RestAmount -= coins[i];
        }
    }

    // Check if exact change is possible
    if (RestAmount == 0) {
        printf("\n");
    } else {
        // If not possible, print a message
        printf("\nExact change not possible.\n");
    }
}

int main() {
    // Example usage
    int GivenCoins[] = {25, 10, 5, 1};
    int numCoins = sizeof(GivenCoins) / sizeof(GivenCoins[0]);
    int TrgtAmt = 64;

    GreedyCoinCh(GivenCoins, numCoins, TrgtAmt);

    return 0;

}
Scroll to Top