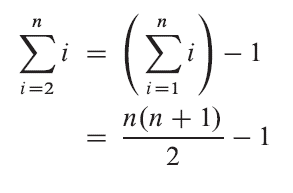- What are the “Stages of algorithm development?
- What an algorithm can do or capabilities of an algorithm?
- Algorithms as a Technology?
- Correctness of an algorithm.
- How to analyzing algorithms? The underlying RAM(Random access machine)model.
The stages of an algorithm refer to the steps or phases involved in the development and execution of an algorithm to solve a specific problem.
Informally, an algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output in a finite amount of time. An algorithm is thus a sequence of computational steps that transform the input into the output. You can also view an algorithm as a tool for solving a well-specified computational problem.
- Stages of algorithm development
The statement of the problem specific in general terms the desired input/output relationship for problem instances, typically of arbitrarily large size. The algorithm describes a specific computational procedure for achieving that input/output relationship for all problem instances. As an example, suppose that you need to sort a sequence of numbers into monotonically increasing order. This problem arises frequently in practice and provides fertile ground for introducing many standard design techniques and analysis tools. Here is how we formally define the sorting problem:
Let’s consider a simple example of finding the maximum number in an array as an illustration of these stages.
- Describing the Problem:
The problem is to find the maximum number in an array of integers.
- Identifying a Suitable Technique:
For this problem, a straightforward technique is to iterate through the array and keep track of the maximum number encountered so far.
Designing the Algorithm (Example Code in C):
#include <stdio.h>
int findMax(int arr[], int size) {
if (size <= 0) {
return -1; // If the array is empty or invalid size
}
int maxNum = arr[0]; // Initialize maxNum with the first element
for (int i = 1; i < size; i++) { // Iterate through the array starting from the second element
if (arr[i] > maxNum) {
maxNum = arr[i]; // Update maxNum if a larger number is found
}
}
return maxNum;
}
int main() {
int array[] = {5, 9, 3, 7, 11, 2};
int size = sizeof(array) / sizeof(array[0]);
int maximum = findMax(array, size);
if (maximum != -1) {
printf("The maximum number in the array is: %d\n", maximum);
} else {
printf("The array is empty or invalid.\n");
}
return 0;
}
This C code follows a similar approach to the Python example:
- findMax function iterates through the array to find the maximum number.
- main() function initializes an array, calculates its size, calls findMax, and prints the result.
When we shall call an algorithm is correct?
An algorithm is correct if it solves the problem for every input, finishing its work in a reasonable time and giving the right answer. A right algorithm solves the problem well. Sometimes, a wrong algorithm won’t finish or will give the wrong answer. Contrary to what you might expect, incorrect algorithms can sometimes be useful, if you can control their error rate.
2. Algorithms’ capability
Problems Solved by Algorithms
- Beyond Sorting: Algorithms address various computational problems, seen in practical applications.
Practical Applications:
- Human Genome Project: Identifying genes, determining DNA sequences, storing data, and analysing it all require intricate algorithms. Dynamic programming aids in similarity determination between DNA sequences, saving time and resources.
- Internet Management: Managing data flow and search engines utilize algorithms to find optimal data routes and locate specific information efficiently.
- Electronic Commerce: Security in online transactions relies on algorithms like public-key cryptography, ensuring privacy and secure exchanges.
- Resource Allocation in Enterprises: Linear programming models aid in allocating resources effectively for various purposes, from maximizing profits in oil companies to optimizing campaign spending for political candidates.
Specific Problem-Solving Techniques Covered:
- Shortest Route Determination: Using graphs to find the shortest path between intersections.
- Topological Sorting: Organizing parts in a mechanical design efficiently
- Medical Imaging: Utilizing clustering algorithms to identify cancerous or benign tumors, discussed.
- File Compression: Techniques like LZW and Huffman coding reduce file sizes efficiently.
Common Characteristics of Algorithmic Problems:
- Many Solutions: Most potential solutions don’t solve the problem; finding the right or optimal one is challenging without examining each possibility.
- Practical Utility: Many problems have real-world applications. For instance, finding the shortest path benefits transportation firms, routing nodes on the internet, or individuals using navigation apps.
Varied Applications:
- Signal Processing: Discrete Fourier Transform (DFT) converts time-domain signal samples into the frequency domain. Its applications range from signal processing to data compression
Algorithms as a Technology
- Termination and Accuracy: Even with infinitely fast computers and free memory, studying algorithms remains crucial to ensure methods terminate correctly and yield accurate solutions.
- Efficiency Matters: Despite faster computers, time and memory remain limited resources. Choosing algorithms efficiently utilizing these resources is crucial.
- Efficiency Variation: Algorithms for the same problem can vary significantly in efficiency. For instance, insertion sort takes time roughly proportional to c1.n2, while merge sort takes time roughly proportional to c2.nlogn.
- Impact of Efficiency: In a comparison between insertion sort and merge sort on different computers, the difference in algorithm efficiency becomes evident. Even with a slower computer, a more efficient algorithm performs significantly better.
- Algorithms vs. Hardware: Algorithm efficiency impacts total system performance as much as fast hardware. As problem sizes increase, the advantage of efficient algorithms becomes more pronounced.
- Role of Algorithms in Modern Technologies:
- Algorithms play a vital role in various computer technologies, including hardware design, graphical user interfaces, networking, and programming languages.
- Fields like machine learning and data science heavily rely on algorithms, which form the core of these disciplines.
- Algorithmic Knowledge: While some tasks can be accomplished without in-depth algorithmic knowledge, a solid understanding of algorithms significantly enhances a programmer’s capabilities, especially as computers handle larger problems.
3. Loop invariants and correctness of an algorithm
Loop invariants play a crucial role in understanding the correctness of algorithms like insertion sort. In insertion sort, the loop invariant essentially guarantees that the sub-array to the left of the current index remains sorted during each iteration of the outer loop. This invariant ensures that as the algorithm progresses, the sorted portion of the array gradually expand until the entire array is sorted. At each step within the loop, the algorithm correctly places the current element in its appropriate position within the already sorted sub array, maintaining the overall sorted order. This consistency and adherence to the loop invariant across iterations affirm the correctness of the insertion sort algorithm.

In computer science, a loop invariant is a condition that is true before and after each iteration of a loop in an algorithm. It helps in understanding the correctness of an algorithm and proving that it works as intended. For insertion sort, the loop invariant plays a crucial role in ensuring that the algorithm correctly sorts the elements.
Loop Invariant: The loop invariant for the inner while loop is that elements to the left of the current j index within the array A (from A[1] to A[i-1]) are sorted in ascending order.
Correctness of Insertion Sort:
- Initialization: At the start of the algorithm, when i = 2, the first element A[1] (considered as a sorted subarray) trivially satisfies the loop invariant because a single element is always sorted.
- Maintenance: As the algorithm proceeds, for each iteration of the outer loop, the inner while loop shifts elements larger than the key value to the right, creating space for the key in the sorted subarray. The key value is correctly placed at the appropriate position within the sorted subarray A[1:i].
- Termination: When the outer loop completes (i = n), all elements have been considered and inserted into their correct positions. The entire array A is now sorted in ascending order.
The key steps to note are:
- The key value is compared with elements in the sorted subarray (A[1:i-1]) and inserted at the correct position within this subarray.
- Elements greater than the key are shifted one position to the right to accommodate the key.
This process guarantees that after each iteration, the subarray A[1:i] remains sorted, leading to the entire array being sorted once the outer loop finishes. Therefore, the loop invariant holds throughout the execution of the algorithm, ensuring the correctness of the insertion sort algorithm in sorting the given array A of size n.
Ref. The below questions have been taken from the book “Introduction to Algorithm”, Coremen et al.
- Exercise a): Using the bellow Figure as a model(also using above insertion sort pseudocode), illustrate the operation of INSERTION-SORT on an array initially containing the sequence <31, 41, 59, 26, 41, 58>.

- Exercise b) . Consider the procedure SUM-ARRAY on the facing page. It computes the sum of the n numbers in array A[1:N]. State a loop invariant for this procedure, and use Its initialization, maintenance, and termination properties to show that the SUMARRAY procedure returns the sum of the numbers in A [1:N].
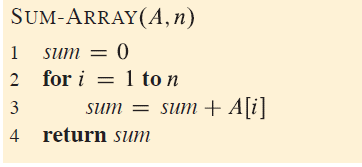
Exercise c). Rewrite the INSERTION-SORT procedure to sort into monotonically decreasing instead of monotonically increasing order.
Exercise d).

- Exercise e).
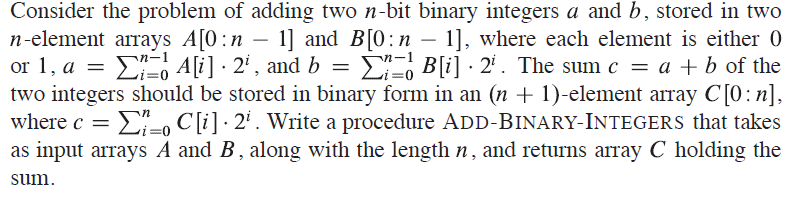
- Exercise f)

- Write a C code for the above algorithm and highlight with logic that loop invariant is maintained.
5. Analyzing algorithms: The underlying RAM(Random access machine)model
Algorithm analysis involves predicting resource requirements, predominantly computational time, among other factors like memory, communication bandwidth, and energy consumption. Comparing multiple algorithms for a specific problem allows for the identification of the most efficient one while eliminating inferior options. To conduct an analysis, a model of the technology supporting the algorithm is essential. Typically, the analysis assumes a one-processor, random-access machine (RAM) model, where instructions execute sequentially and uniformly, simplifying computations. However, this model overlooks deviations from real-world computers, necessitating caution. While it assumes constant time for operations and data access, real computers possess additional instructions and nuances not accounted for, creating a gray area in analysis. Precision in floating-point values, limitations on word sizes, and scenarios like exponentiation or shifting bits are accommodated within assumptions but might deviate from real-world scenarios.
The RAM model, fundamental for algorithm analysis, does not consider the memory hierarchy common in modern computers, omitting factors like caches and virtual memory. Despite its limitations, the RAM model remains a strong predictor of real-world performance. However, analyzing algorithms within this model can be challenging, often requiring mathematical tools such as combinatorics, probability theory, and the ability to distill complex behaviors into simple formulas. As algorithms can exhibit varying behaviors based on inputs, summarizing these behaviors becomes crucial for analysis. While the RAM model serves as a foundational tool, it’s essential to acknowledge its limitations and potential disparities with real computing systems when conducting algorithmic analyses.
6. Time analysis of insertion sort