Huffman codes are highly effective for data compression, typically achieving savings between 20% and 90%, depending on the nature of the data being compressed. The input data consists of a sequence of characters. Huffman’s greedy algorithm constructs an optimal binary representation for each character by utilizing a frequency table that indicates how often each character appears.
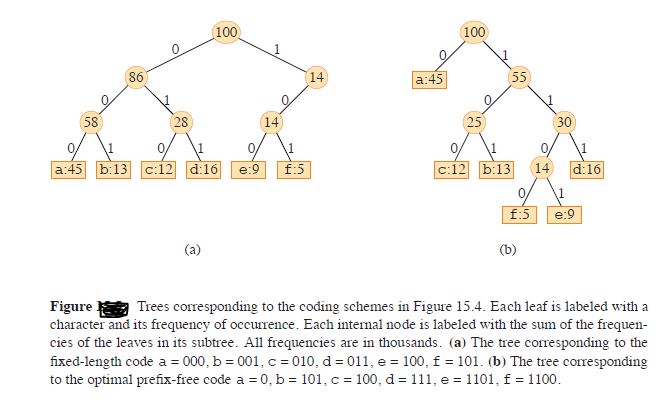
Imagine you have a data file containing 100,000 characters that you want to store efficiently. The file consists of 6 unique characters, each appearing with the frequencies shown in Figure 15.4. For instance, the character ‘a’ appears 45,000 times, ‘b’ appears 13,000 times, and so forth. There are various ways to encode this information, but here, we focus on creating a binary character code (or simply a code) to represent it. In a fixed-length code, each character requires ⌈log2n⌉\lceil \log_2 n \rceil⌈log2n⌉ bits to represent n≥2n \geq 2n≥2 characters. For 6 characters, this means 3 bits are needed per character: a=000,b=001,c=010,d=011,e=100,f=101a = 000, b = 001, c = 010, d = 011, e = 100, f = 101a=000,b=001,c=010,d=011,e=100,f=101. Using this approach, encoding the entire file would require 300,000 bits. Is there a more efficient solution?
A variable-length code offers significant improvement over fixed-length coding. The concept is straightforward: assign shorter code-words to frequently occurring characters and longer codewords to less common ones. For example, in bellow Figure the 1-bit code 0 represents a, while the 4-bit code 1100 represents f. Using this variable-length scheme, the file can be encoded in (45⋅1+13⋅3+12⋅3+16⋅3+9⋅4+5⋅4)⋅1,000=224,000 bits, achieving a savings of approximately 25%. This approach is, in fact, the optimal character coding for this file, as we will demonstrate.





#include <stdio.h>
#include <stdlib.h>
// Define the structure for a Huffman Tree node
typedef struct Node {
int freq;
struct Node *left, *right;
} Node;
// Function to create a new node
Node* createNode(int freq) {
Node* node = (Node*)malloc(sizeof(Node));
node->freq = freq;
node->left = node->right = NULL;
return node;
}
// Function to extract the node with the minimum frequency
Node* extractMin(Node** nodes, int* size) {
int minIndex = 0;
for (int i = 1; i < *size; i++) {
if (nodes[i]->freq < nodes[minIndex]->freq)
minIndex = i;
}
Node* minNode = nodes[minIndex];
nodes[minIndex] = nodes[--(*size)];
return minNode;
}
// Huffman Tree construction function
Node* buildHuffmanTree(int* freq, int n) {
Node* nodes[n];
for (int i = 0; i < n; i++) nodes[i] = createNode(freq[i]);
int size = n;
while (size > 1) {
Node* x = extractMin(nodes, &size);
Node* y = extractMin(nodes, &size);
Node* z = createNode(x->freq + y->freq);
z->left = x;
z->right = y;
nodes[size++] = z;
}
return nodes[0];
}
// Function to print the tree (pre-order traversal)
void printTree(Node* root, int depth) {
if (!root) return;
printf("%*sFreq: %d\n", depth * 2, "", root->freq);
printTree(root->left, depth + 1);
printTree(root->right, depth + 1);
}
int main() {
int freq[] = {5, 9, 12, 13, 16, 45};
int n = sizeof(freq) / sizeof(freq[0]);
Node* root = buildHuffmanTree(freq, n);
printf("Huffman Tree (pre-order traversal):\n");
printTree(root, 0);
return 0;
}
output:
Huffman Tree (pre-order traversal):
Freq: 100
Freq: 45
Freq: 55
Freq: 25
Freq: 12
Freq: 13
Freq: 30
Freq: 14
Freq: 5
Freq: 9
Freq: 16