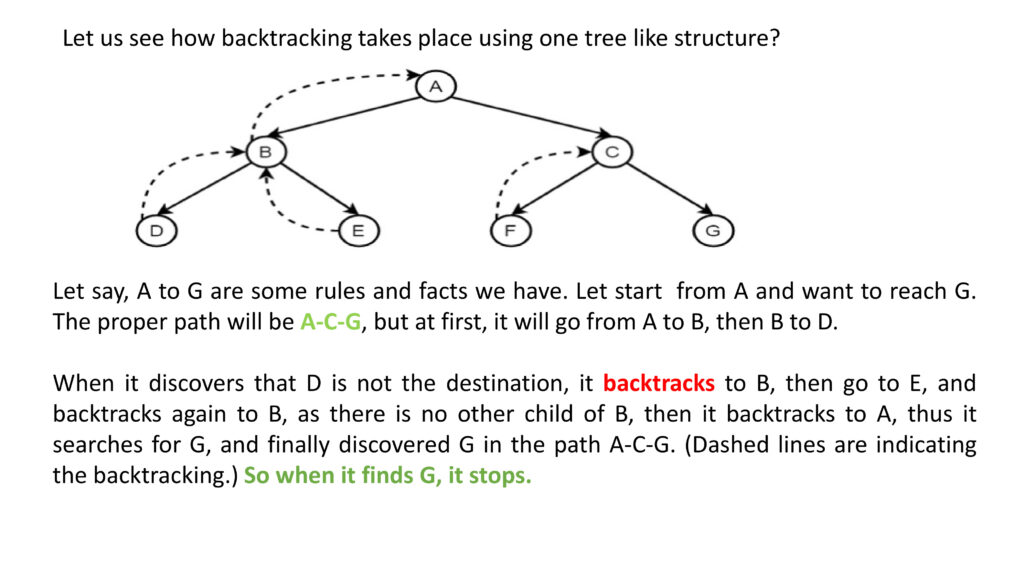
- How does back tracking work?
- How to solve the N Queen problem by backtracking?
- How to solve the subset sum problem(or Sum of Subsets) by backtracking?
- How to solve the graph colouring problem by backtracking?
- Rat in a Maze problem-solving by backtracking


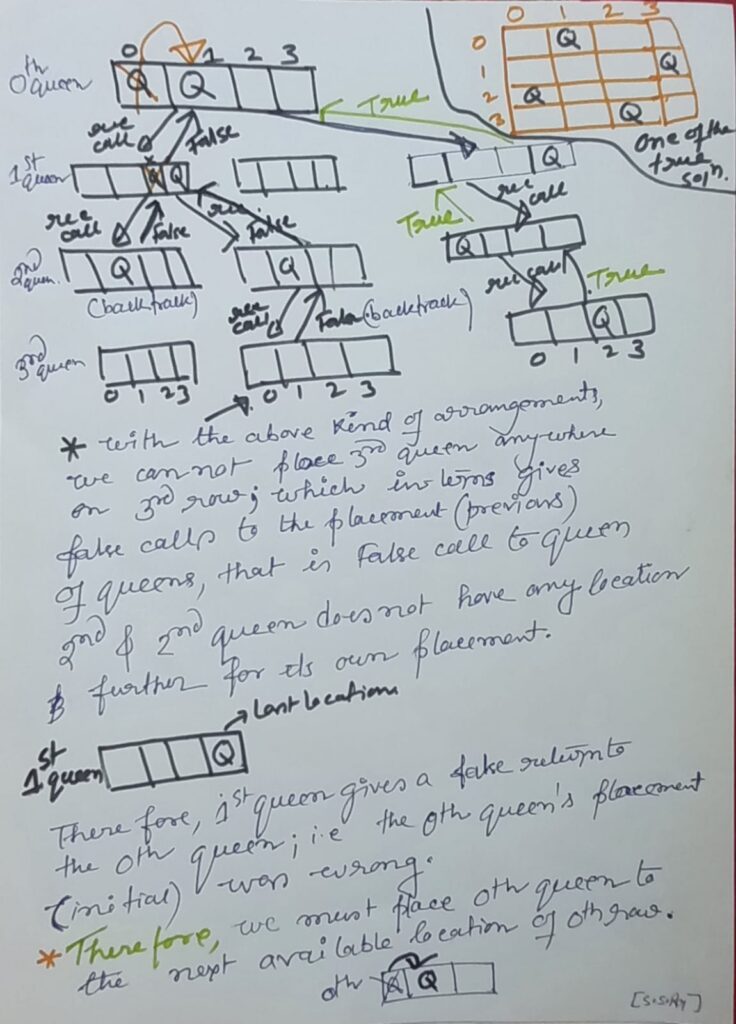
Solving N Queen problem by Backtracking

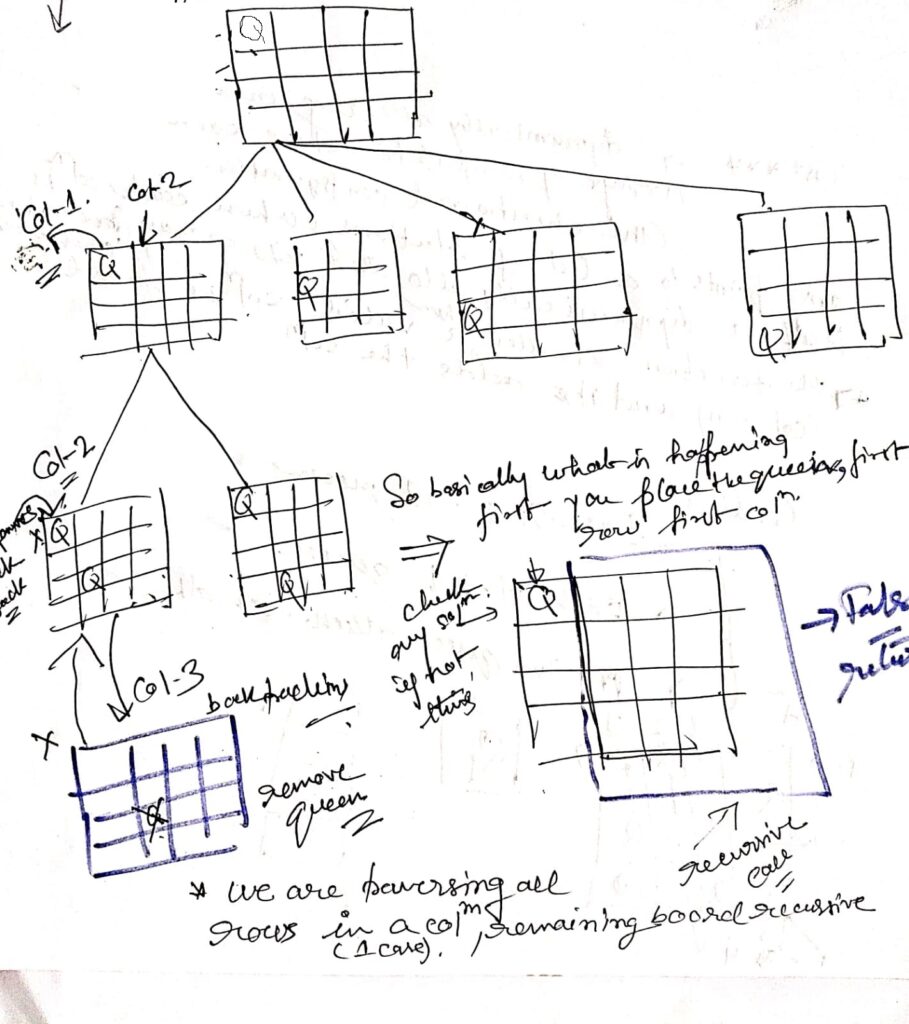
// C program : Backtracking solution for N-Queen problem
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// Function to add the current solution to the answer list
void addSolution(int*** ans, int** board, int* solutionCount, int n) {
(*solutionCount)++;
*ans = (int**) realloc(*ans, (*solutionCount) * sizeof(int*));
(*ans)[*solutionCount - 1] = (int*) malloc(n * n * sizeof(int));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
(*ans)[*solutionCount - 1][i * n + j] = board[i][j];
}
}
}
// Function to check if it is safe to place a queen at board[row][col]
bool isSafe(int row, int col, int** board, int n) {
int x = row, y = col;
// Check the left row
while (y >= 0) {
if (board[x][y] == 1)
return false;
y--;
}
// Check the upper left diagonal
x = row, y = col;
while (x >= 0 && y >= 0) {
if (board[x][y] == 1)
return false;
x--;
y--;
}
// Check the lower left diagonal
x = row, y = col;
while (x < n && y >= 0) {
if (board[x][y] == 1)
return false;
x++;
y--;
}
return true;
}
// Function to solve the N-Queens problem
void solve(int col, int*** ans, int** board, int* solutionCount, int n) {
if (col == n) {
addSolution(ans, board, solutionCount, n);
return;
}
for (int row = 0; row < n; row++) {
if (isSafe(row, col, board, n)) {
// Place queen if it's safe
board[row][col] = 1;
solve(col + 1, ans, board, solutionCount, n);
// Backtrack
board[row][col] = 0;
}
}
}
// Function to print the solutions
void printSolutions(int** solutions, int solutionCount, int n) {
for (int k = 0; k < solutionCount; k++) {
printf("Solution %d:\n", k + 1);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
printf("%c ", solutions[k][i * n + j] == 1 ? 'Q' : '.');
}
printf("\n");
}
printf("\n");
}
}
// Main function to find all N-Queens solutions
int main() {
int n;
printf("Enter the value of N: ");
scanf("%d", &n);
// Allocate memory for the board
int** board = (int**) malloc(n * sizeof(int*));
for (int i = 0; i < n; i++) {
board[i] = (int*) calloc(n, sizeof(int));
}
// Initialize solution list
int** solutions = NULL;
int solutionCount = 0;
// Solve the problem
solve(0, &solutions, board, &solutionCount, n);
if (solutionCount == 0) {
printf("No solutions exist for N = %d.\n", n);
} else {
printf("Total solutions for N = %d: %d\n\n", n, solutionCount);
printSolutions(solutions, solutionCount, n);
}
// Free allocated memory
for (int i = 0; i < n; i++) {
free(board[i]);
}
free(board);
for (int i = 0; i < solutionCount; i++) {
free(solutions[i]);
}
free(solutions);
return 0;
}
Output :
Enter the value of N: 4
Total solutions for N = 4: 2
Solution 1:
. . Q .
Q . . .
. . . Q
. Q . .
Solution 2:
. Q . .
. . . Q
Q . . .
. . Q .
Process returned 0 (0x0) execution time : 2.579 s
Press any key to continue.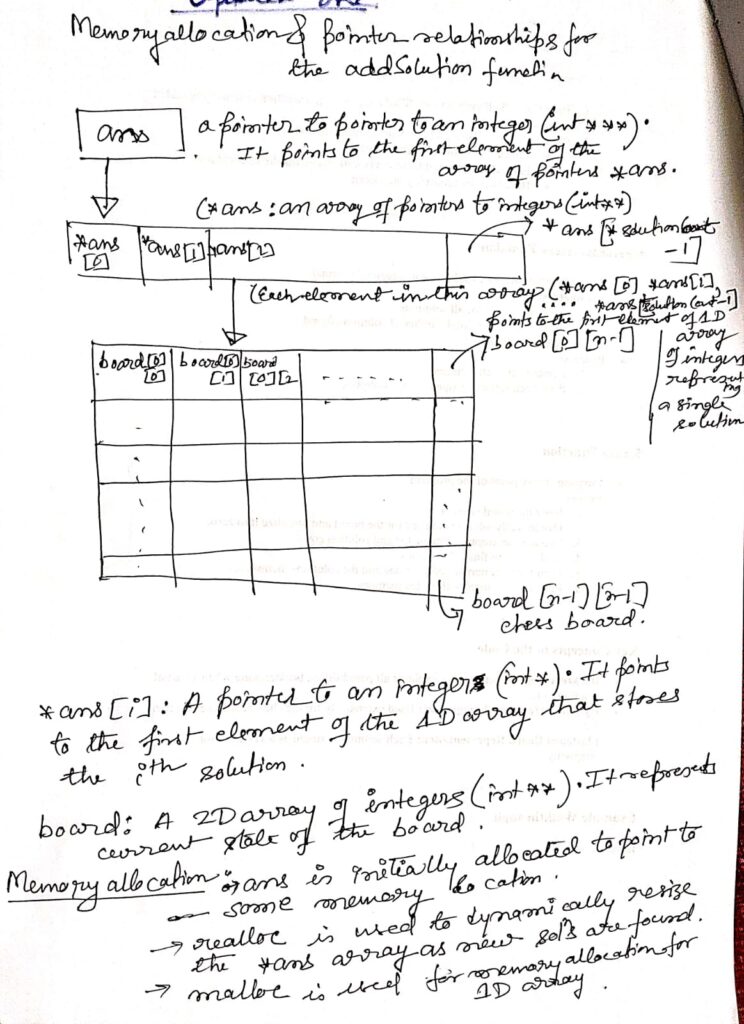
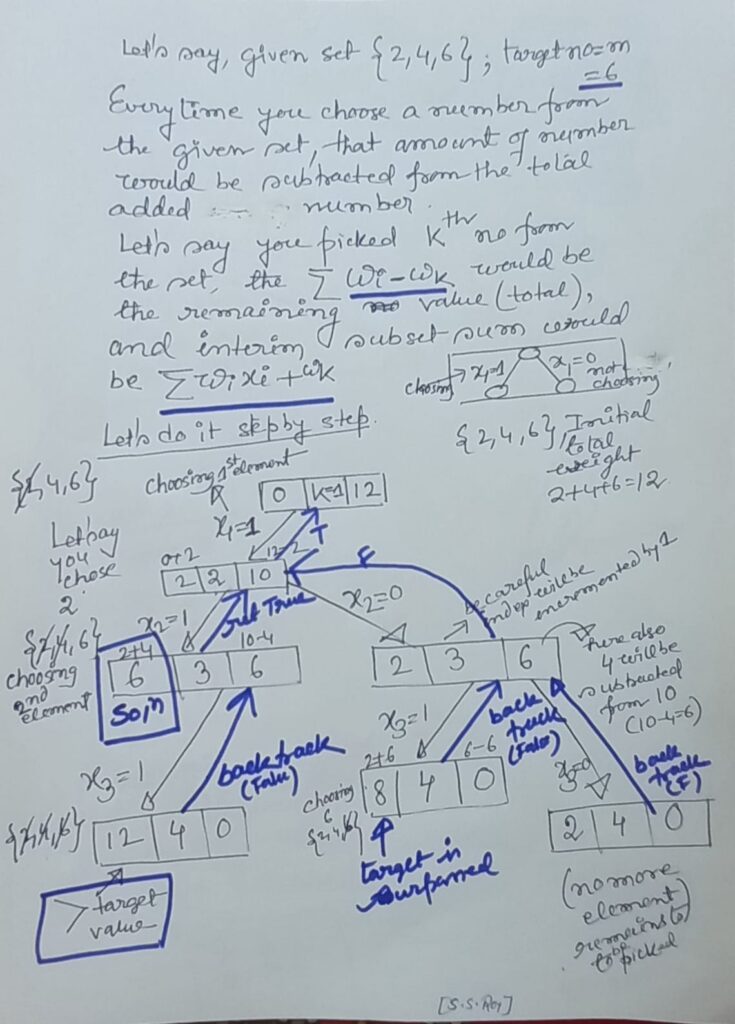
Solving Subset sum problem(or Sum of Subsets) by Backtracking

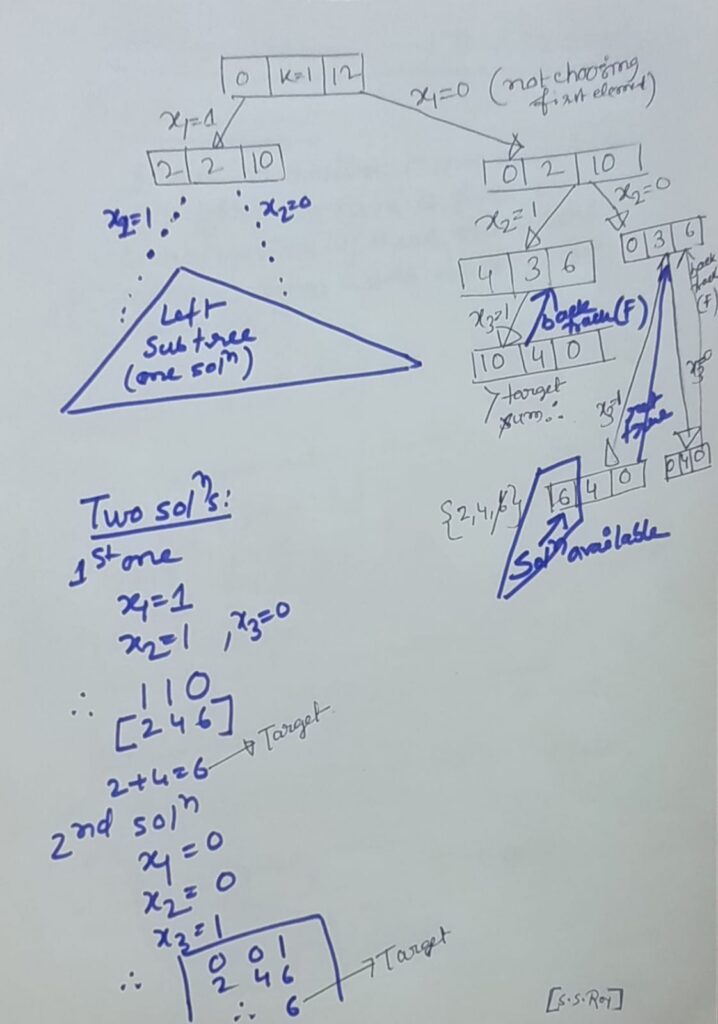
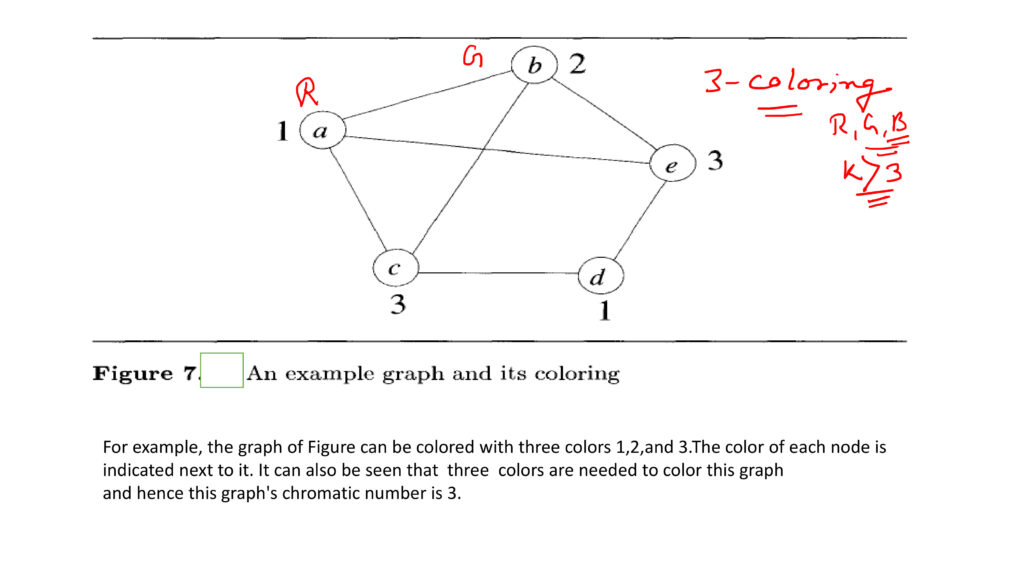
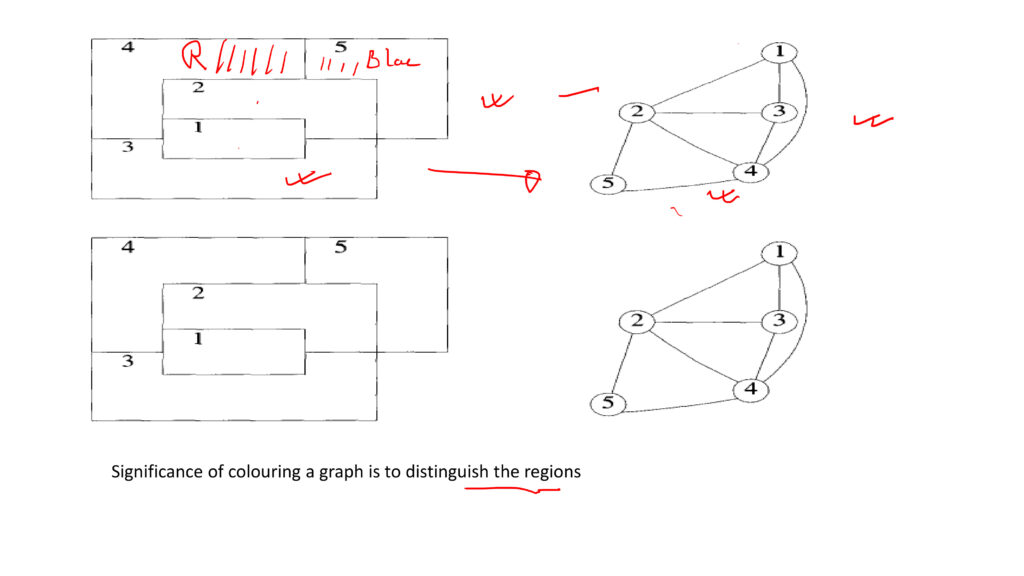
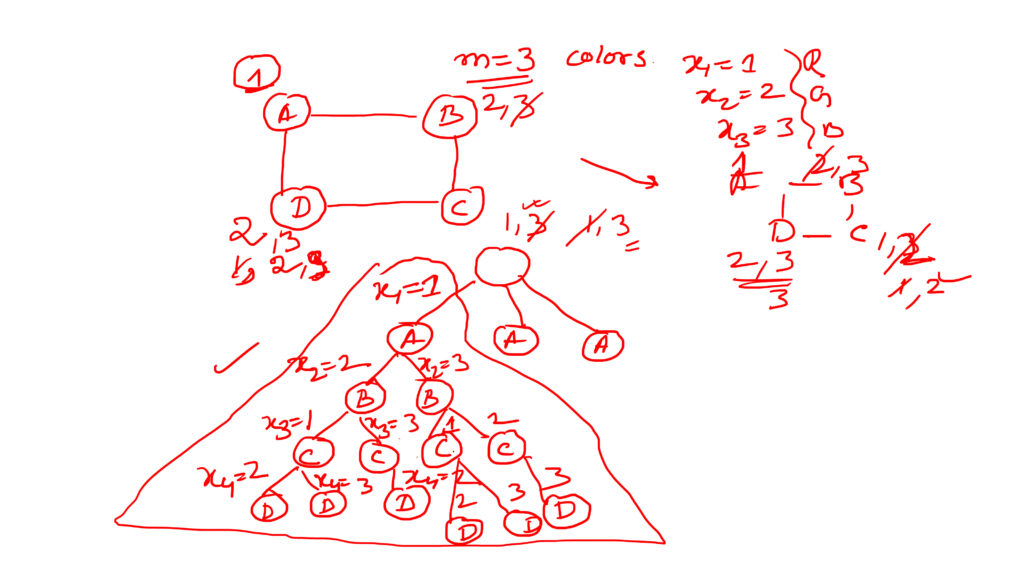
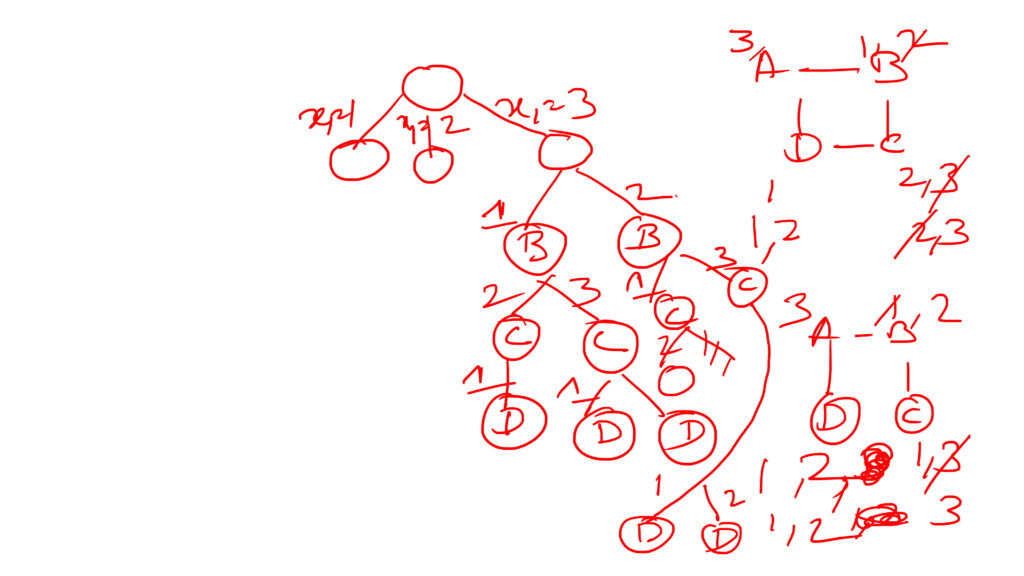
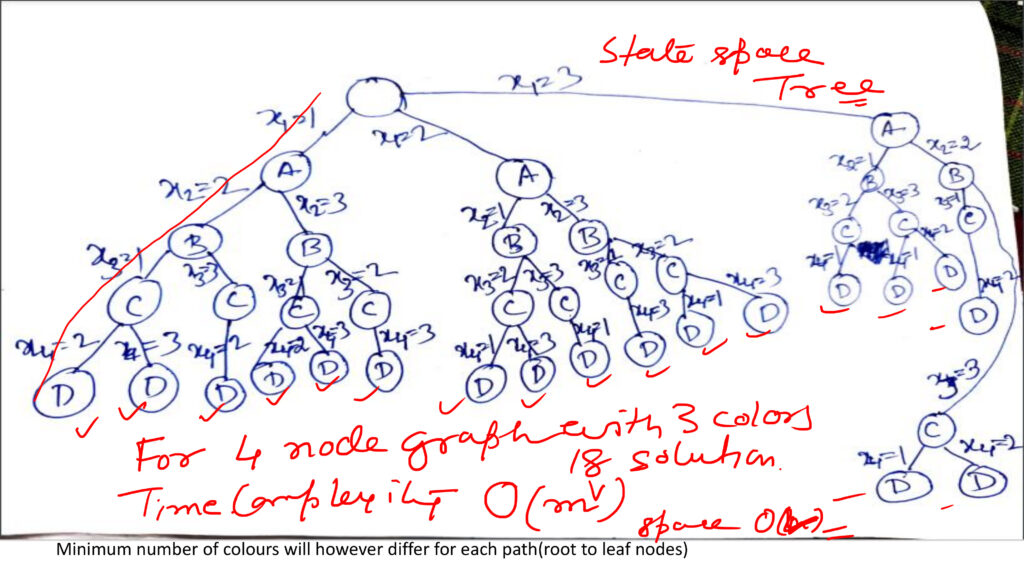
Solving graph colouring problem by back tracking


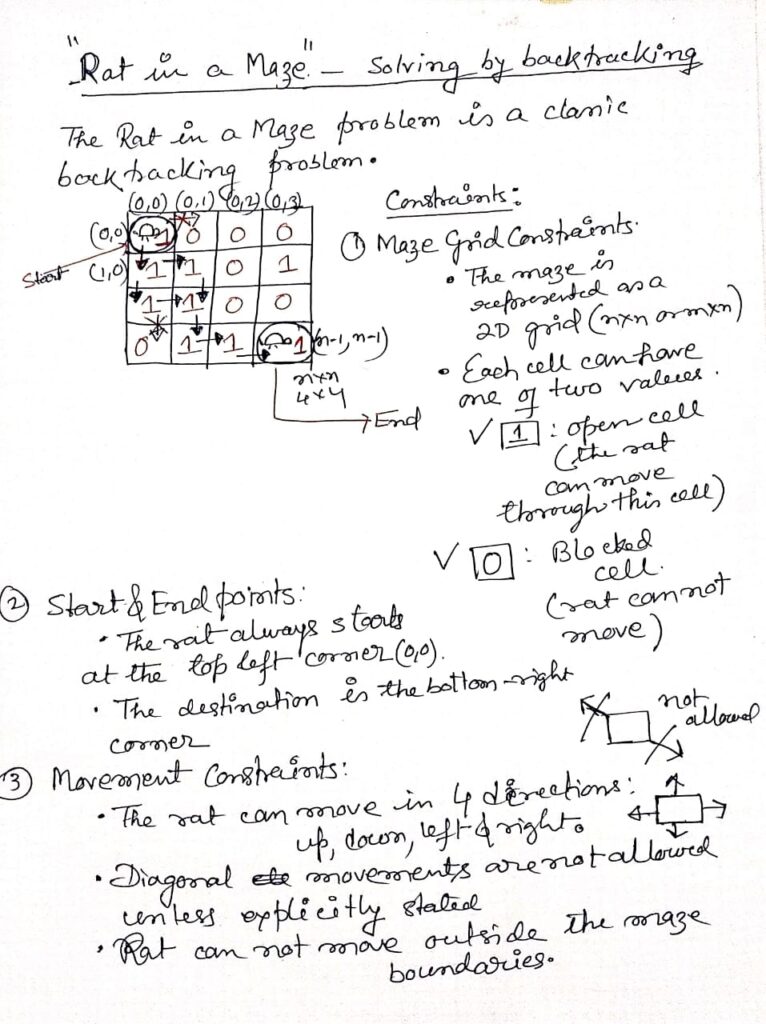
Rat in a Maze problem-solving by backtracking
The Rat in a Maze problem is a classic backtracking problem where a rat is placed in a maze and needs to find a path to reach the destination. The maze is represented by a grid of cells, where some cells are blocked, and others are open for movement. The goal is to determine all possible paths or at least one path from the source (top-left corner) to the destination (bottom-right corner).

//C++ backtracking solution for Rat in a Maze problem.
#include <iostream> // Include the iostream library for input/output operations
#include <vector> // Include the vector library for using dynamic arrays
using namespace std;
// Checks if a given cell (x, y) is valid for the rat to move to.
bool isSafe(int x, int y, int n, vector<vector<int>>& maze, vector<vector<int>>& sol) {
return (x >= 0 && x < n && y >= 0 && y < n && maze[x][y] == 1 && sol[x][y] == 0);
}
// Recursive function to solve the maze
bool solveMaze(int x, int y, int n, vector<vector<int>>& maze, vector<vector<int>>& sol, vector<pair<int, int>>& path) {
// Base case: Reached the destination
if (x == n - 1 && y == n - 1) {
sol[x][y] = 1; // Mark destination as visited
path.push_back({x, y}); // Add destination coordinates to the path
return true;
}
// Check if the current cell is valid
if (isSafe(x, y, n, maze, sol)) {
// Mark current cell as visited
sol[x][y] = 1;
path.push_back({x, y}); // Add current coordinates to the path
// Explore all possible directions (right, down, left, up)
if (solveMaze(x + 1, y, n, maze, sol, path) ||
solveMaze(x, y + 1, n, maze, sol, path) ||
solveMaze(x - 1, y, n, maze, sol, path) ||
solveMaze(x, y - 1, n, maze, sol, path)) {
return true; // If any direction leads to a solution, return true
}
// Backtrack (if no solution found in any direction)
sol[x][y] = 0; // Unmark the cell
path.pop_back(); // Remove coordinates from the path
return false;
}
return false; // If the cell is not safe, return false
}
// Prints the coordinates of the solution path
void printSolution(vector<pair<int, int>>& path) {
cout << "Solution Path Coordinates:" << endl;
for (auto coord : path) {
cout << "(" << coord.first << ", " << coord.second << ") ";
}
cout << endl;
}
int main() {
int n;
cout << "Enter the size of the maze: ";
cin >> n;
vector<vector<int>> maze(n, vector<int>(n));
cout << "Enter the maze (1 for open path, 0 for blocked):" << endl;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> maze[i][j];
}
}
vector<vector<int>> sol(n, vector<int>(n, 0)); // Initialize solution matrix with 0s
vector<pair<int, int>> path;
if (solveMaze(0, 0, n, maze, sol, path)) {
cout << "Solution found:" << endl;
printSolution(path);
} else {
cout << "No solution exists." << endl;
}
return 0;
}
Output :
Enter the size of the maze: 4
Enter the maze (1 for open path, 0 for blocked):
1 0 1 0
0 1 0 1
1 1 0 1
1 1 1 1
No solution exists.
*********************************************
Enter the size of the maze: 4
Enter the maze (1 for open path, 0 for blocked):
1 0 1 1
1 1 0 1
1 1 1 1
0 0 1 1
Solution found:
Solution Path Coordinates:
(0, 0) (1, 0) (2, 0) (2, 1) (2, 2) (3, 2) (3, 3)//C code implementation of backtracking for solving Rat in a Maze problem
#include <stdio.h>
#include <stdlib.h>
#define MAX 100
// Checks if a given cell (x, y) is valid for the rat to move to.
int isSafe(int x, int y, int n, int maze[MAX][MAX], int sol[MAX][MAX]) {
return (x >= 0 && x < n && y >= 0 && y < n && maze[x][y] == 1 && sol[x][y] == 0);
}
// Recursive function to solve the maze
int solveMaze(int x, int y, int n, int maze[MAX][MAX], int sol[MAX][MAX], int path[MAX][2], int *pathIndex) {
// Base case: Reached the destination
if (x == n - 1 && y == n - 1) {
sol[x][y] = 1; // Mark destination as visited
path[*pathIndex][0] = x;
path[*pathIndex][1] = y;
(*pathIndex)++;
return 1;
}
// Check if the current cell is valid
if (isSafe(x, y, n, maze, sol)) {
// Mark current cell as visited
sol[x][y] = 1;
path[*pathIndex][0] = x;
path[*pathIndex][1] = y;
(*pathIndex)++;
// Explore all possible directions (right, down, left, up)
if (solveMaze(x + 1, y, n, maze, sol, path, pathIndex) ||
solveMaze(x, y + 1, n, maze, sol, path, pathIndex) ||
solveMaze(x - 1, y, n, maze, sol, path, pathIndex) ||
solveMaze(x, y - 1, n, maze, sol, path, pathIndex)) {
return 1; // If any direction leads to a solution, return true
}
// Backtrack (if no solution found in any direction)
sol[x][y] = 0; // Unmark the cell
(*pathIndex)--;
return 0;
}
return 0; // If the cell is not safe, return false
}
// Prints the coordinates of the solution path
void printSolution(int path[MAX][2], int pathIndex) {
printf("Solution Path Coordinates:\n");
for (int i = 0; i < pathIndex; i++) {
printf("(%d, %d) ", path[i][0], path[i][1]);
}
printf("\n");
}
int main() {
int n;
printf("Enter the size of the maze: ");
scanf("%d", &n);
int maze[MAX][MAX];
printf("Enter the maze (1 for open path, 0 for blocked):\n");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &maze[i][j]);
}
}
int sol[MAX][MAX] = {0}; // Initialize solution matrix with 0s
int path[MAX][2]; // To store the path coordinates
int pathIndex = 0;
if (solveMaze(0, 0, n, maze, sol, path, &pathIndex)) {
printf("Solution found:\n");
printSolution(path, pathIndex);
} else {
printf("No solution exists.\n");
}
return 0;
}
Output :
Enter the size of the maze: 4
Enter the maze (1 for open path, 0 for blocked):
1 0 1 0
0 1 0 1
1 1 0 1
1 1 1 1
No solution exists.
*********************************************
Enter the size of the maze: 4
Enter the maze (1 for open path, 0 for blocked):
1 0 1 1
1 1 0 1
1 1 1 1
0 0 1 1
Solution found:
Solution Path Coordinates:
(0, 0) (1, 0) (2, 0) (2, 1) (2, 2) (3, 2) (3, 3)