The maximum sum subarray problem involves finding a contiguous portion of an array that yields the highest possible sum of its elements.
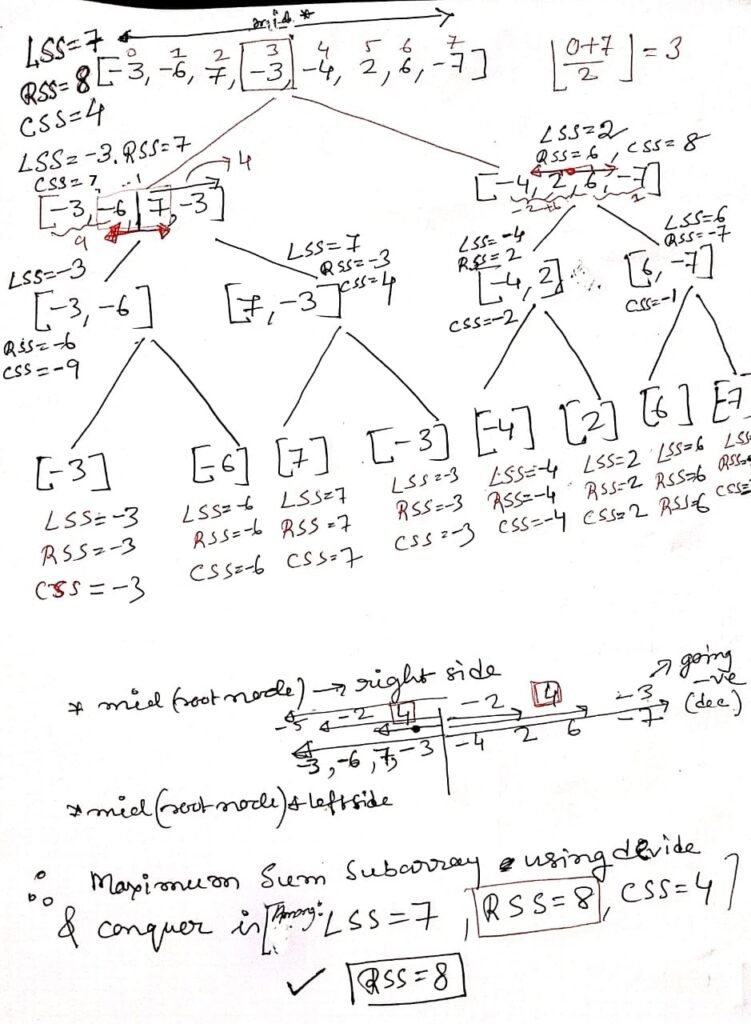
To solve the maximum sum subarray problem using the brute force method, you calculate the sum of all possible subarrays and keep track of the maximum sum found. Here’s an example with a diagram:
Example:
Array: [1, -2, 3, 4, -1, 2]
- Brute Force Approach:
- Generate all subarrays.
- Calculate the sum of each subarray.
- Track the maximum sum.



#include <stdio.h> // Includes the standard I/O library for input and output operations.
#include <limits.h> //Includes limits.h for the definition of INT_MIN (the smallest integer value).
// Function to find the maximum sum of a subarray that crosses the midpoint
int maxCrossingSum(int arr[], int low, int mid, int high) { // Defines a function to calculate the maximum sum of a subarray crossing the midpoint.
int left_sum = INT_MIN, right_sum = INT_MIN;// Initializes variables to store the maximum sums of the left and right subarrays.
//INT_MIN is a constant defined in the limits.h header file in C,
//which represents the smallest possible value
// that can be stored in a variable of type int on the current platform.
int sum = 0;// Initializes a variable to accumulate the sum for left and right subarrays.
// Find the maximum sum on the left of mid
for (int i = mid; i >= low; i--) { // Loops through the left subarray from mid to low.
sum += arr[i]; // Adds the element at index i to the sum.
if (sum > left_sum) //Compares the current sum with left_sum.
left_sum = sum; // Updates left_sum if the current sum is greater.
}
sum = 0; // Resets sum for the right subarray.
// Find the maximum sum on the right of mid
for (int i = mid + 1; i <= high; i++) { // Loops through the right subarray from mid + 1 to high.
sum += arr[i]; // Adds the element at index i to the sum.
if (sum > right_sum) // Compares the current sum with right_sum.
right_sum = sum; // Updates right_sum if the current sum is greater.
}
// Return the maximum of the three parts
return left_sum + right_sum;//Returns the sum of the left and right maximum subarrays
//crossing the midpoint.
}
// Function to find the maximum sum subarray using divide and conquer
int maxSubArraySum(int arr[], int low, int high) { // Defines a function to calculate the maximum subarray sum using divide and conquer.
if (low == high) { // Base case: If there's only one element in the subarray.
return arr[low]; // Return the single element as the maximum sum.
} else {
int mid = (low + high) / 2;// Finds the midpoint of the array to divide the array into two halves.
// Recursively find the maximum sum in the left half, right half, and crossing the mid
int left_sum = maxSubArraySum(arr, low, mid);// Recursively finds the maximum subarray sum in the left half.
int right_sum = maxSubArraySum(arr, mid + 1, high);// Recursively finds the maximum subarray sum in the right half.
int cross_sum = maxCrossingSum(arr, low, mid, high);// Finds the maximum subarray sum that crosses the midpoint.
// Return the maximum of the three sums
if (left_sum >= right_sum && left_sum >= cross_sum) // Compares the three sums and returns the largest.
return left_sum;
else if (right_sum >= left_sum && right_sum >= cross_sum) // Compares and returns the right sum if it's the largest.
return right_sum;
else // Returns the crossing sum if it's the largest.
return cross_sum;
}
}
int main() { // The main function where execution begins.
int arr[] = {−3,−6,7,−3};
//int arr[] = {-2, 1, -3, 4, -1, 2, 1, -5, 4}; // Initializes the array with sample values.
int n = sizeof(arr) / sizeof(arr[0]);// Calculates the number of elements in the array.
int max_sum = maxSubArraySum(arr, 0, n - 1);//Calls the divide-and-conquer function to find the maximum subarray sum.
printf("Maximum subarray sum is: %d %d\n", max_sum,cross_sum);// Prints the maximum subarray sum.
return 0; // Returns 0 to indicate successful execution.
}
/*
Output :
Maximum subarray sum is: 6
Process returned 0 (0x0) execution time : 0.017 s
Press any key to continue.
**************************************************************************************************
Some Key Points :
- **Libraries**:
- `stdio.h`: For input/output operations (e.g., printing).
- `limits.h`: For `INT_MIN`, which represents the minimum possible integer value.
- **Functions**:
- `maxCrossingSum`: Finds the maximum sum of a subarray that crosses the midpoint.
- `maxSubArraySum`: Implements divide-and-conquer to find the maximum subarray sum by recursively breaking the array into halves and calculating the sum for each half and crossing subarray.
- **Main function**: Initializes the array, calls the divide-and-conquer function, and prints the result.
*/