The following topics have been discussed
- Why Greedy Algorithm?
- What are the three key points of Greedy method?
- How to solve Job sequencing problem using greedy method?
Greedy Algorithms: Making Optimal Choices
In optimization problems, algorithms often undergo multiple steps, presenting various choices at each juncture. While dynamic programming might be the go-to for some optimization challenges, employing simpler and more efficient methods becomes paramount for many scenarios. This is where the essence of greedy algorithms shines through.
Why Greedy Algorithm?
A greedy algorithm adheres to a simple principle: make the choice that appears to be the best at that precise moment. It traverses a path of locally optimal choices, aiming that these cumulative decisions culminate into a globally optimal solution.
Three Key Ingredients of Greedy Method
1. Greedy-Choice Property
The foundation of a greedy algorithm lies in its ability to assemble an overall optimal solution by consistently selecting locally optimal choices. Essentially, at every decision point, the algorithm opts for the choice that seems most favourable within the context of the current problem. This decision doesn’t delve into outcomes or solutions of sub-problems.
2. Optimal Substructure
The presence of optimal substructure signifies that the optimal solution to a problem encompasses optimal solutions to its sub-problems. In a greedy algorithm, the path taken involves making immediate choices that seem optimal, subsequently resolving the remaining sub-problems. Importantly, the choices made in a greedy algorithm may rely on preceding choices but cannot be influenced by future choices or sub-problem solutions.
3. Recursive or Iterative Solution Development
To implement a greedy algorithm, two primary approaches exist: either through a recursive or an iterative method. The choice of the method depends on the nature of the problem and the preferred strategy for implementation.
Greedy Algorithms in Action
A characteristic of a greedy algorithm is its decisiveness. Unlike dynamic programming, which resolves sub-problems before initiating the primary decision-making process, a greedy algorithm makes its initial choice upfront, before delving into any sub-problem solutions.

While dynamic programming ascends from solving sub-problems in a bottom-up manner, a greedy strategy takes a top-down route. It sequentially makes optimal choices, reducing the complexity of the original problem with each decision.
In essence, the charm of greedy algorithms lies in their ability to make locally optimal decisions, trusting that these choices will harmoniously lead to a globally optimal solution. This method’s efficiency and simplicity make it an invaluable tool in a wide array of optimization challenges.
Job sequencing problem : solving by greedy method
In the world of job sequencing problems, where the goal is to optimize the order in which tasks are scheduled, the Greedy Method emerges as a strategic and intuitive approach. This method follows a simple yet effective principle: make the locally optimal choice at each step with the hope of finding a globally optimal solution. Let’s delve into the fundamentals of the Greedy Method as applied to the job sequencing problem.
Problem Statement:
Consider a scenario where there are multiple jobs with associated deadlines and profits. The objective is to schedule these jobs in a way that maximizes the total profit, given the constraint that each job must be completed within its deadline. The challenge is to find an optimal order of execution that ensures the highest overall profit.
The Greedy Algorithm:
- Sort Jobs by Profit: Begin by sorting the jobs in descending order based on their profits. This step ensures that the job with the highest profit comes first.
- Assign Jobs to Time Slots: Initialize a time slot array and iterate through the sorted jobs. For each job, find the latest available time slot before its deadline and assign the job to that slot.
- Calculate Total Profit: Calculate the total profit by summing up the profits of the assigned jobs.
Key Considerations:
- Local Optimization: At each step, the algorithm makes a locally optimal choice by selecting the job with the highest profit available. This might not always lead to the globally optimal solution, but it often yields satisfactory results.
- Deadline Constraint: The algorithm ensures that each job is assigned within its specified deadline, respecting the constraints of the problem.
Let’s consider an example to illustrate the Greedy Method for the job sequencing problem. Assume we have the following set of jobs with associated profits and deadlines:
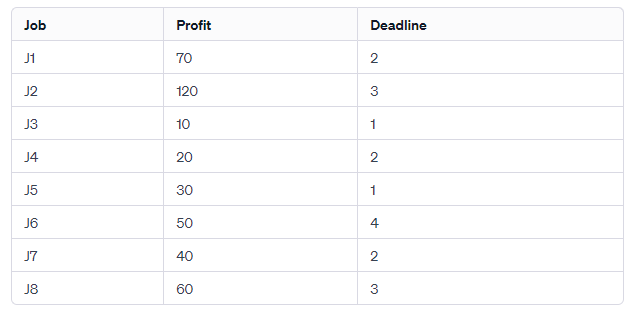
Step 1: Sorting by Profit in Descending Order
Sorting the jobs in descending order based on profit gives us:

Step 2: Assigning Jobs to Time Slots
Initialize a time slot array and assign jobs to available slots based on their deadlines. The latest available time slot before the deadline is chosen.
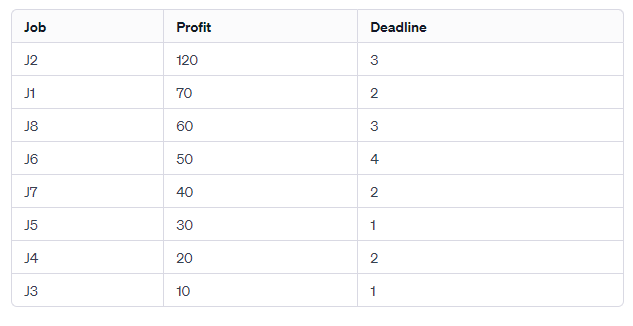
Step 3: Total Profit Calculation
Calculate the total profit by summing up the profits of the assigned jobs:
Total Profit = 120 + 70 + 60 + 50 + 40 + 30 = 370
Therefore, following the Greedy Method, the optimal sequence of job execution results in a total profit of 370. This example demonstrates how the Greedy Method efficiently maximizes profit while adhering to deadline constraints in a job sequencing problem.